Arithmetic Progression

Arithmetic Progression

If we observe then we may notice that there is some pattern in some things like 2,4,6,8 are all even numbers and the difference is same that is two. It means on adding 2 in each even number we get a new even number. Same things happen with odd numbers also. Like this there a lot of patterns. So, let’s learn more about the topic and patterns.

As the name suggest Arithmetic means adding or subtracting and progression means series.

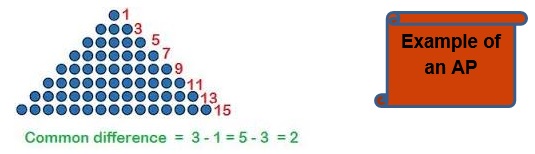
A sequence of numbers such that the difference between the consecutive term is constant then the sequence is said to be in Arithmetic Progression.

For example 3,7,11,15,19,23. Here each term differs the previous term by 4 and since the difference is constant therefore it is a arithmetic progression.

• The constant difference is actually known as common difference and is denoted by d.
• The first term of an AP is denoted by a.

Therefore the general form of an Arithmetic Progression is a, a+d, a+2d, a+3d, a+4d………….n times.

• Here we can notice that the common difference between each term is d.

Common Difference:

The common difference can be positive, negative or even zero.

• If the difference is positive then the AP is called increasing AP. For example 2, 12, 22, 32, 42, 52.
• If the difference is negative then the AP is called decreasing AP. For example 12, 10, 8, 6, 4.
• If the difference is zero then it is called as constant AP. For example 5, 5, 5, 5, 5, 5, 5, 5.

If we denote the first term by a_1, second term by a₂  and so on therefore the n^th  term will be a_n. Then the AP hence formed will be a₁, a₂, a₃, ……………..a_n.

So, a₂-a₁ = a₃-a₂ = a₄-a₃ ………..= a_n-a_n-1 = d.

N^th Term of an AP

It is not always possible to determine all the terms of an AP if it contains a lot of terms. For example if we have to determine the 1000^th term of an AP of even nos then it is not that easy and also time taking.

Hence we generalize the result to find the n^th term of an AP

Let a₁, a₂, a₃, ……………..a_n, be an AP of n terms and here a₁ is the first term and d is common difference.

a₂ = a + d = a + (2-1)d

a₃ = a+2d = a + (3-1)d

a₄ = a+3d= a + (4-1)d

Similarly

General Term a_n =  a + (n-1)d  

And the last term of AP l = a + (n-1)d if there are n term

Example1:- Find the 10^th term of the AP 2,12, 22, 32….

Solution:- Here first term a = 2 and common difference d is

12-2 = 10 = d.

Using the formula and putting n=10 we get

a₁₀ = 2+ (10-1)10 = 2 + 90 = 92.

Example 2:- Which term of the AP 15,10, 5, 0 … will be -40?

Solution:- Here a =15 and d = -5.

And here as we know that a_n = -40.

On putting the values in the formula we get

-40 = 15 + (n-1)(-5)

-55 = (n-1)(-5)

Therefore (n-1) = 11 and hence n = 12.

So the 12^th term will be -40.

Sum of N terms of an AP

Let us consider an AP with first term a and common difference d

a, a+d, a+2d, a+3d, a+4d………………………a+(n-1)d.

Let S denotes the sum of the first n terms and therefore

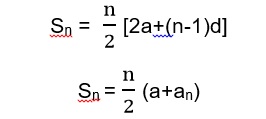
• Here an important point is to remembered that a_n = S_n-S_n-1.

It means that the n^th term of an AP is equal to the difference of its sum of n^th and sum of (n-1)^th term.

Example 3:- Find the sum of 10 terms of the AP -3, 1, 5, 9,13..?

Solution:-  Here a = -3 and d = 4

Therefore on putting the values in the formula we get

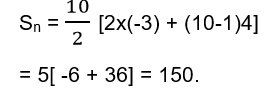
Hence the sum of first 10 terms is 150.

Word Problems

Example 4:- Raman started working at a company at an annual salary of Rs 5000 per year and he received an annual increment of Rs 200 per year. After how many years his salary will be Rs 8000?

Solution:- Here the sequence will be 5000, 5200, 5400, 5800, 6000……….8000

Here the first term a =5000 and d=200, a_n = 8000

On using the formula and putting the values in it, we get

8000 = 5000 +(n-1)200

3000 = (n-1)200 and hence (n-1) = 15

Therefore n= 16 which means after 16 years Raman’s annual salary will be Rs 8000 per year.

Example 5:- A contract company has to pay penalty if the works get delayed. Rs 100 for first day, Rs 150 for second, Rs 200 for third and so on. Find out how much money the contractor has to pay if the work gets delayed by 30 days.

Solution:- The sequence formed will be 100 , 150, 200, 250 …

 Here a=100 and d=50 and n=30

Therefore on putting the values in the formula we get,

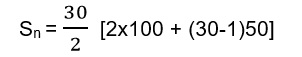
S_n = 15[200+1450]

S_n = 15 x 1650 = 24750.

Hence the contractor has to pay Rs 24,750 as penalty for the delay of work for 30 days.

Practice Questions

Q1) Write the first four terms of the AP if

1. a= 3 and d=5 ii) a=12 and d=-2         

• a=4 and d=-2 iv) a=10 and d= 10

Q2) Find a₁, a₂, a₄  and d of the following AP

1. 10, 5, 0, -5,-10 ….. b) -20,-12,-4, 4…..

Q3) Find the n^th term of the following AP

1. 5, 11, 17, 23, 29…….
2. 10, 15 ,20, 25 ……….

Q4) Determine the AP whose first term is 8 and 3^rd term is 24.

Q5) How many two digit numbers are divisible by 5?

Q6) Find the sum first 200 even integers.

Recap

• The sequence having a common difference is known as AP.

• The general term is a_n = a+(n-1)d

• The common difference d can be positive or negative or zero also.
• The addition, subtraction, multiplication or division of two AP’s also results in an AP.