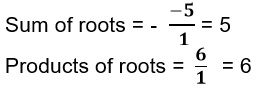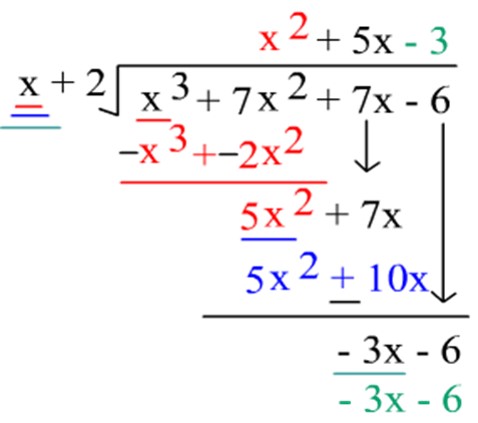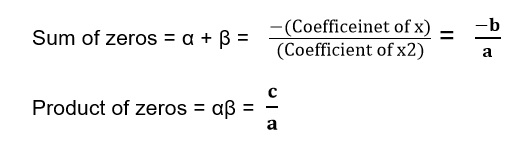Every day we all undergo through a lot of expressions with single or multiple variables like 4x+y=2, 9x+ 12, etc. Here one thing is to be noticed that if an expression contains only one variable the solutions and analysis of the expression will be different rather than for a multiple variable expression. Here we are going to learn some of the basic concepts of expressions in one variable only.
A polynomial is an expression of several terms of different powers of a same variable undergoing algebraic operations.
For example: x2+9x+12, 4x+2, etc.
If p(x) is a polynomial in x, then the highest power of x in p(x) is called as degree of the polynomial.
A polynomial of degree one is called as linear polynomial, with degree two is quadratic; with degree three is cubic polynomial. For example 4x+5 is a linear polynomial, x2+3x+2 is a quadratic polynomial, x3+3x2-2x+4 is a cubic polynomial.
If p(x) is a polynomial in x, and if k is any real number, then the value obtained by replacing x by k in p(x), is called the value of p(x) at x = k, and is denoted by p(k).
More generally, a real number k is said to be a zero of a
Polynomial p(x), if p(k) = 0
Significance of Zeros of Polynomial
We all know that for every equation or expression that can be written on the paper can also be represented graphically on the Cartesian plane.
So if we try to plot the linear, quadratic and cubic polynomial we will end up in a line for linear, a parabola for quadratic and another curve for cubic polynomial as well.
Thus when we start plotting the curves on the Cartesian plane we require the different coordinates to determine from where the curve would pass
Thus the zeroes here helps us in determining how many times the curve will cut the X axis.
Example 1: Identify the number of zeros of the following graphs.
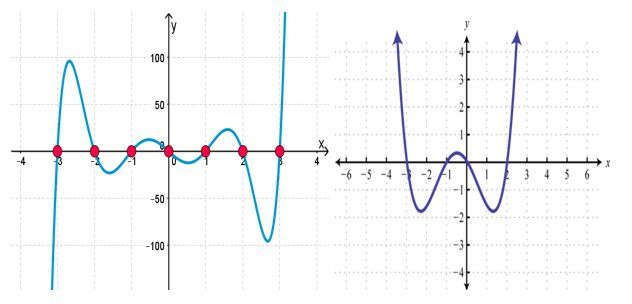
Solution:
The first graph has 7 zeros which are -3,-2,-1,0,1,2,3
The second graph has 4 zeros which are
-3,-1, 0 and 2.
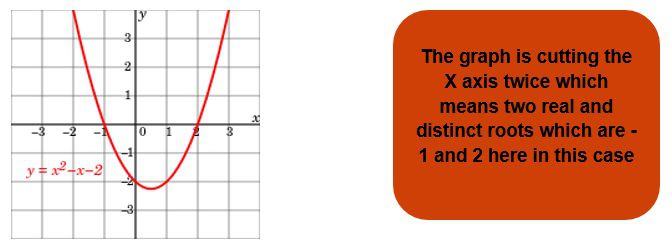
If we consider a quadratic polynomial ax2+bx+c then it will have at most two zeros known as α and β, and these two zeros have some special property:
Example 1: Find the sum and product of the roots of the quadratic equation x2-5x+6. Solution: On comparing the quadratic equation with the general form we get a=1, b=-5, c=6. Therefore, Division Algorithm Dividend = Divisor x Quotient + Remainder If p(x) and g(x) are any two polynomials with g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that p(x) = g(x) × q(x) + r(x) This result is known as Division Algorithm Example 3: Find the values of remainder and quotient when x3+7x2+7x-6 is divided by x+2. Solution: Here we know that the value of dividend is x3+7x2+7x-6 and the value of the divisor is x+2. On applying the division method and on using the formula: Dividend = Divisor x Quotient + Remainder Here we get that Quotient is x2+5x-3 and remainder is -3x-6.
Practice Questions Q1) If any polynomial cuts the X axis 3 times and touches it for 2 times then how many zeros does this polynomial has? Q2) If any polynomial cuts the X axis 2 times and the Y axis 5 times. Then how many zeros are there of the polynomial? Q3) Find the sum and product of the roots of the following polynomials: Q4) Find the value of the remainder and quotient when the polynomial x4-5x+6 is divided by 2-x2. Recap For an quadratic equation ax2+bx+c Dividend = Divisor x Quotient + Remainder