• A quadrilateral is a 4-sided polygon, just like a triangle is a 3-sided polygon, a pentagon is a 5-sided polygon, and so on. A quadrilateral has 4 edges (sides) and 4 vertices (corners).

Polygons

• A polygon can be defined as a geometric object consisting of a number of points and an equal number of line segments.

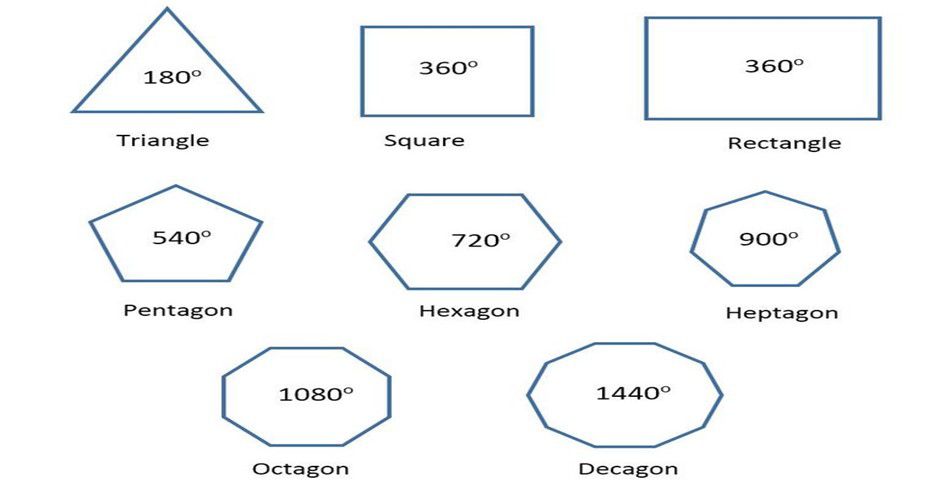
Types of Polygons:
Regular Polygon: All angles are equal and all sides are the same length. Regular polygons are both equiangular and equilateral.
Convex Polygon: A straight line drawn through a convex polygon crosses at most two sides. Every interior angle is less than 180 degrees.
Concave Polygon: We can draw at least one straight line through a concave polygon that crosses more than two sides. At least one interior angle is more than 180 degrees.

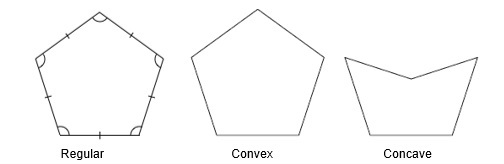
• Polygon Parts:
  Side: One of the line segments that make up the polygon.
  Vertex: Point where two sides meet.
  Diagonal: A line connecting two vertices that isn’t a side.
  Exterior Angle: The exterior angle is the angle between any side of a shape, and a line extended from the next side. Each Exterior Angle= 360°/N
  Interior Angle: Angle formed by two adjacent sides inside the polygon. The interior angle and the exterior angle add up to 180 degrees.
  Apothem: A line from the centre of a regular polygon at a right angle to any of its
  Area of a regular polygon= perimeter X apothem/2

Sum of the measure of exterior angle of polygon

We will learn now how to find the sum of exterior angles of a polygon having n sides.
We know that, exterior angle + interior adjacent angle = 180°
So, if the polygon has n sides, then
Sum of all exterior angle + Sum of all interior angle = n X 180°
So, sum of all exterior angle= n X 180° - sum of all interior angle
= n X 180° - (n-2) X 180°
=n X 180° - (n X 180°) +(2 X 180°)
= 360°

Each Exterior Angle= 360°/n
Number of sides of a polygon= 360°/(each exterior angle)

EXAMPLE 1: The exterior angles of a quadrilateral are (m+1) °, (2m+3) °, (4m+5) °, (5m +6) °. Find the measure of each angle.

SOLUTION: We know that sum of all exterior angle= 360°
Therefore, (m+1) + (2m+3) + (4m+5) + (5m+6)= 360°
12m + 15 = 360°
12m = 345
m= 345/12
m= 28.75

(m+1) = (28.75+1) = 29.75°
(2m+3) = (2X28.75+3) = 60.5°
(4m+5) = 120°
(5m+6) = 149.75°
Hence, the measure of each exterior angles is 29.75°, 60.5°, 120°, 149.75°.

EXAMPLE 2: The sum of the interior angles of a regular polygon is 3 times the sum of its exterior angles. Determine the number of sides of the polygon.

SOLUTION: Sum of interior angles of a regular polygon is 3 times the sum of exterior angles. [Given]

We know that in a regular polygon sum of all the exterior angles is 360°

Therefore, the sum of interior angles= 3 X 360°= 1080°

Again, we have sum of interior angles = (n-2) X 180°, where n is the number of sides of the polygon.
(n-2)180° = 1080°

(n-2)=1080°/180°

n = 6 + 2

n = 8 [Ans]

Kinds of Quadrilaterals

• Parallelogram: Opposite sides are parallel and congruent. Opposite angles are congruent. Adjacent angles are supplementary. Diagonals bisect each other and each diagonal divide the parallelogram into two congruent triangles. If one of the angles of a parallelogram is right angle then all other angles are a right angle and the parallelogram becomes a rectangle.

Area = Length X Height
Perimeter = 2X (length + breadth)

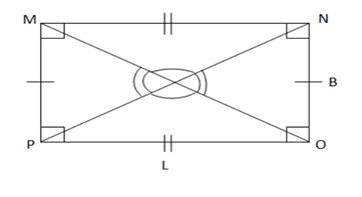
• Rectangle: Opposite sides are parallel and congruent. All angles are right. The diagonals are congruent and bisect each other. Opposite angles formed at the point where diagonals meet are congruent. A rectangle is a special type of parallelogram whose angles are right.
  Length of Diagonal =

Area = Length X Breadth

Perimeter= 2X (Length+Breadth)

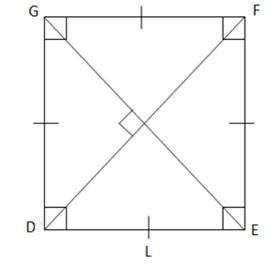
• Squares: All sides and angles are congruent. Opposite sides are parallel to each other. The diagonals are congruent. The diagonals are perpendicular to and bisect each other. A square is a special type of parallelogram whose all sides and angles are equal.

Length of Diagonal = Length
Area= (length)²

Perimeter= 4Xlength

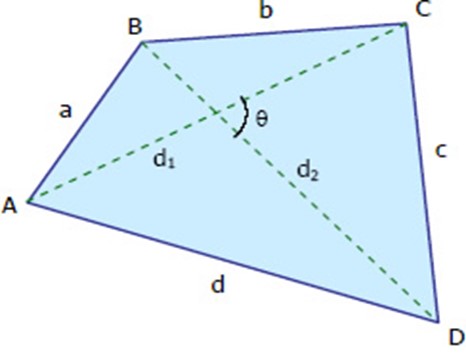
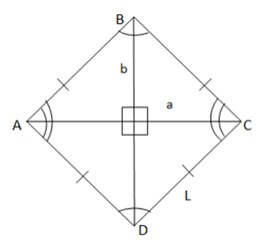
• Rhombus: All sides are congruent. Opposite angles are congruent. The diagonals are perpendicular to and bisect each other. Adjacent angles are supplementary. A rhombus is a parallelogram whose diagonals are perpendicular to each other.
  Area = (aXb)/2
  Perimeter= 4 X length

• Trapezium: The bases of the trapezium are parallel to each other. No sides, angles, and diagonals are congruent.
  Area = ½ X h X (L+L₂₎
  Perimeter = L + L₁ + L₂ + L₃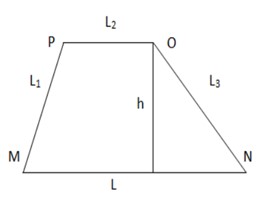
• 

EXAMPLE 1: Calculate the area of a parallelogram whose height is 1m and base is 2m.

SOLUTION: Area= Base X Height= 1 X 2= 2m²

EXAMPLE 2: Calculate the area of a trapezium whose height is 3m and length of two parallel sides are 4m and 5m respectively.

SOLUTION: Area= ½ X h X (L1+L2) = ½ X 3 X (4+5) = 0.5 X 3 X 9 = 13.5m²

Constructing a quadrilateral

• When 4 sides and 1 diagonal are given:
  Construct a quadrilateral ABCD with AB=3cm, BC=5cm, CD=4.5cm, AD=4cm, and the length of diagonal is AC= 7cm.
  
  Step1: Draw a line segment AC of 7cm.

Step2: With 3cm as a radius from A draw an Arc.
Step3: With 5 cm as radius cut the arc drawn in Step2. Let that point of intersection be B. Join AB and CB
Step4: With 4 cm as a radius from A draw an arc to the opposite side of AC.
Step5: From C take 4.5cm as radius and cut the arc drawn in Step4. Let the point of intersection be D. Join AD and CD

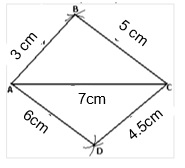
• When 3 sides and two diagonals are given:
  Construct the quadrilateral PQRS in which PQ=3cm, QR=2cm, PS=1.5cm, PR=3.5cm, QS=3cm
  
  Step1: Draw a line segment PQ=3cm
  Step2: With 3.5cm from P draw an arc.
  Step3: From Q take a radius of 2cm and cut the arc drawn in Step2. Let the point of intersection be R.
  Step4: Take 1.5cm from P and draw an Arc.
  Step5: Take 3 cm from Q and cut the arc drawn in Step4.
  Step6: Join SR.

PQRS is the required quadrilateral.

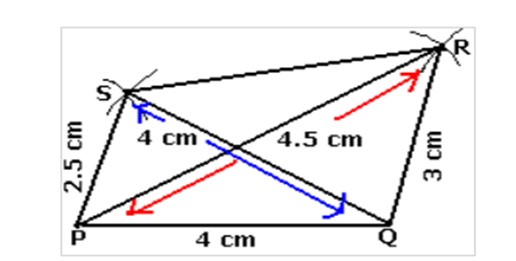
• When 4 sides and one angle are given:
  Construct a trapezoid ABCD in which AB|| CD, AB=7cm and BC=5cm
  CD=3cm and angle B= 60°

In a trapezoid ABCD, AB||CD,
B + C = 180°
C= 180° - B = 180° - 60° = 120°

Step1: Draw AB= 7cm
Step2: At B, draw = 60°

Step3: From ray BX, cut off BC=5cm

Step4: At C, draw =120°

Step5: From ray CY, cut off CD=3cm

Step6: Join D to A.
Step7: ABCD is the required trapezoid

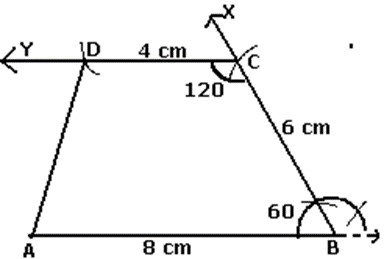
• When 3 sides and their included angles are given:
  Construct a quadrilateral TRUE in which TR=2.5cm, RU= 2cm, UE=3cm, R= 75°, U= 120°

Step1: Draw a line segment of 3cm and an angle of 120° at point U. As vertex E is 3cm away from vertex U, cut a line segment UE=3cm from this ray

Step2: Draw an angle of 75° at point R, as vertex T is 2.5cm away from vertex R, cut a line segment RT of 2.5cm from this ray.

Step3: Join T to E.

TRUE is the required quadrilateral.

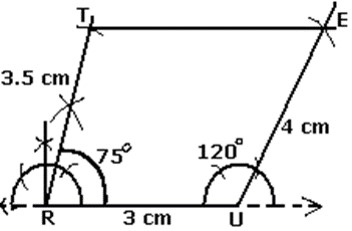
• When 2 adjacent sides and three angles are given:
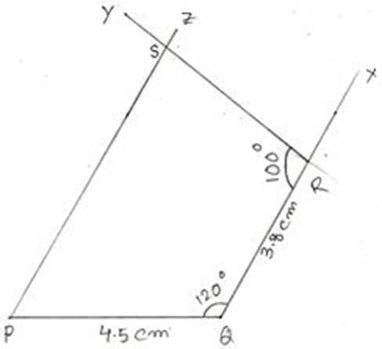
  Construct a quadrilateral PQRS in which PQ=3.5cm, PQR= 120°, QR=2.8cm, QRS=100°, QPS=60°
  
  Step1: Draw PQ=3.5cm
  Step2: Make angle PQX=120°
  Step3: With Q as centre and radius 2.8cm, draw an arc, cutting QX at R. Join QR.
  Step4: Make ∠QRY= 100°
  Step5: ∠QPZ = 60° so that PZ and RY intersect each other at the point S.

Then, PQRS is the required quadrilateral.

Practice these questions

Q1) The angles of a quadrilateral are in the ratio 2:3:4:5. Find the smallest and the largest angle.

Q2) In the adjoining figure, ABCD is a quadrilateral the bisectors of angle A and angle B meet at P. If angle C= 80° and ⦟D= 50°. Find ⦟APB.

Q3) In the adjoining figure, ⦟A= 60°. OE is perpendicular
to AC and OD is perpendicular to AB. Find ⦟DOE.

Q4) Three angles of a quadrilateral are in the ratio 6:7:8. The difference of the least and the greatest of these angle is 51°. Find the angles of the quadrilateral.

Q5) The ratio of two sides of a parallelogram is 9:1 and its perimeter is 23cm. Find the sides of the parallelogram.

Q6) Four sides of a Quadrilateral ABCD as AB = 5cm, BC = 7cm, CD = 6.5cm,AD= 6 cm and one diagonal AC = 9 cm. Construct a quadrilateral.

Q7) Construct a Quadrilateral ABCD in which AB = 5 cm, BC= 4cm, ÐA = 60° , ÐB 105° and ÐC = 105°.

Q8) Construct Quadrilateral ABCD in which AB = 4.5cm, BC = 3.5cm, CD = 5cm, ÐB=45°and ÐC = 150°.

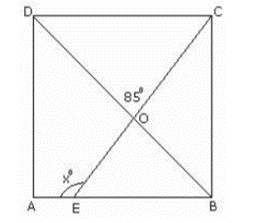
Q9) In the given figure, ABCD is a square. Find the value of x.

Recap

• Sum of angles of a quadrilateral is 360°.
• A diagonal of a parallelogram divides it into two congruent triangles.
• Diagonals of a rectangle bisect each other and are equal and vice-versa.
• Diagonals of a rhombus bisect each other at right angles and vice-versa.
• Diagonals of a square bisect each other at right angles and are equal, and vice-versa.
• We can construct a quadrilateral if we know: four sides and a diagonal, two adjacent sides and three angles, three sides and two diagonals, three sides and two included angles.