We all have been studying this topic from past 3 to 4 years that is from class 6th. Hence we all understand the importance number systems play in the field of mathematics. Here we are going to extend our discussion to the irrationality of numbers and the decimal expansions of the real numbers and some other properties related to real numbers.
Let us go through an overview of classification of numbers first:
- We all know that all the numbers can be of two types
- a) Real Number b) Imaginary Numbers
- Real numbers can be further divided into rational and irrational numbers.
- Rational Numbers are further divided into integers and fractions respectively and integers are further divided into Natural and Whole numbers.
- Numbers which can be written in the form of p/q such that p and q both are integers and q≠0 is called a rational number.
- Hence the real numbers which are not rational are actually irrational numbers.
- There can be infinitely many rational numbers between any two given rational numbers.
Irrational Numbers
- The number which cannot be written in the form of p/q such that p and q are integers and q≠0 is called an irrational number.
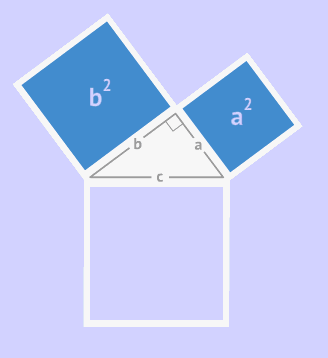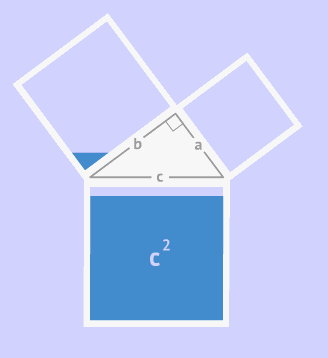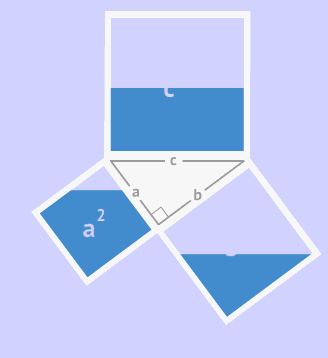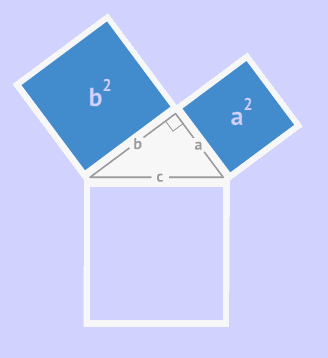
- Pythagoras was the first mathematician to propose and prove the theory of Irrational numbers. He proved that √2 is an irrational number.
- In a number line every real number is represented by a unique and fixed point and every unique point on the number line represents a fixed real number.
Example 1: How to represent √2 on the number line.
Solution: To represent √2 on a number line we will follow the following steps:
- a) Draw a square ABCD of side 1 each.
- b) By Pythagoras theorem AC = √2.
- c) Taking A as center and AC as radius draw an arc such that it intersects the number line at P.
- d) The point P is the required representation of √2 on the number line.
Decimal Expansions of Real Numbers
All those numbers which can be represented on the number line are called as real numbers.
- When we divide a number with another we obtain two results
- a) The remainder finally becomes 0.
- b) The remainder starts repeating itself.
When two number p and q of the form p/q are divided and
Case 1) The remainder finally becomes zero then we say that this type of decimal expansion terminates or ends after finite number of steps and such type of decimal expansion is called as terminating decimal expansions. For example 1/5, 4/9 etc. have remainder zero on division.
Case 2) The remainder never becomes zero then we says that this type of decimal expansion never terminates and hence we call such type of decimal expansion as non-terminating recurring. For example 10/3, 1/9, 1/7, etc. have repetition remainders.
Example 2: Show that 0.666…. can be expressed in the form of p/q where p and q are integers.
Solution: Let us assume that 0.6666… = x
On multiplying both the sides by 10 we get,
10x = 6.66666…
10x = 6 + x (as the number of repetiting 6’s are infinite)
9x = 6 which means x = 2/3.
Hence the number in the form of p/q is 2/3.
From the above examples we can conclude that
- The decimal expansion of any rational number can be either terminating or non-terminating recurring and vice versa.
- The decimal expansion of any irrational number is non- terminating non-recurring and vice versa.
Operations on Real Numbers
- Real numbers satisfy the law of commutative, associative and distributive of addition and multiplication.
- Since irrational numbers are also part of real number and hence like real numbers they also follow the above properties.
- Unlike rational numbers, we cannot predict whether after the operations on irrational numbers, the numbers will be irrational or not.
- An important point is to be remembered that when we do operations on the real numbers, rational part is dealt with the rational part and irrational with the irrational.
- It means that for example when we add two numbers then the rational part will be added with the rational and the irrational part with the irrational.
Hence we can conclude the following things:
- If we add, subtract, multiply or divide two irrational numbers, the result may be an irrational or rational number.
- The sum or difference of a rational and irrational number is irrational.
- The product or division of a non-zero rational number with an irrational number is irrational.
Example 3: Find the product of 5√3 and 2√5.
Solution: On multiplying the rational with rational part and irrational part with irrational we get,
5√3 x 2√5 = 5 x 2 x√3 x√5 = 10 x √15 = 10√15.
Identities of Irrational Numbers
All the rational numbers follow some basic identities which are very helpful in solving the problems.
- √ab = √a√b
- (√a + √b)( √a - √b) = a – b
- (a + √b)(a - √b) = a2 – b
- (√a + √b)2 = a +2√ab +b
Law of Exponents for Real Number
Before heading forward let us revise some of the basic formulae’s.
The below table shows the different laws of exponents and in front of them is a simple illustration explaining the use of law.

Here an important point is to be noticed that the powers are integers that is m and n are integers.
But here we can make the changes and hence we can say that on replacing the integers m and n by rational numbers r and s we get the properties as shown in the following table.

Example 4: Simply and find the following 641/2, 1251/3, 7291/3 .
Solution: Here we can write 64 as 26, therefore the value becomes (2)6/2 = 23 = 8.
We can write 125 as 53 and hence the value becomes 53/3 = 5.
We can write 729 as 93 and hence the value becomes 93/3 = 9.
Practice Questions
Q1) Predict which of the following is rational and which is irrational.
12, √5, √7, √4, √9, 1+2√3, √8-7, 7-√5.
Q2) Which is the smallest natural number? And which is the smallest whole number?
Q3) Represent√5 on the number line.
Q4) Find out which type of decimal expansions are the following:
- a) 1/3 b) 0.444444 c)2/7 d) 1/2
Q5) Represent 0.97979797… in the form of p/q.
- Rational Numbers are further divided into integers and fractions respectively and integers are further divided into Natural and Whole numbers.
- Numbers which can be written in the form of p/q such that p and q both are integers and q≠0 is called a rational number.
- The number which cannot be written in the form of p/q such that p and q are integers and q≠0 is called an irrational number.
- When remainder becomes zero the expansion is terminating and when the remainder does not becomes zero the expansion is called as non-terminating recurring.
- When an irrational number is expanded the expansion is always non-terminating non-recurring.
- If we add, subtract, multiply or divide two irrational numbers, the result may be an irrational or rational number.
- The sum or difference of a rational and irrational number is irrational.
- The product or division of a non-zero rational number with an irrational number is irrational.
- Pythagoras was the first mathematician to propose and prove the theory of Irrational numbers. He proved that √2 is an irrational number.