• Multiple percentages are not additive in nature.

EXAMPLE 1: Two numbers are in the ratio 1:23. On adding 4 to the first and 5 to the second, their ratios become 1:13. Find the numbers.

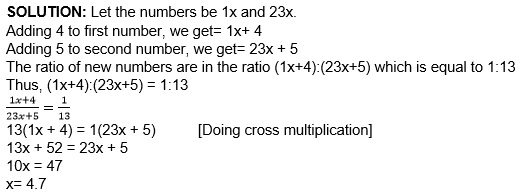
Hence, the numbers are 4.7 and 23X4.7= 108.1 [ANS]

EXAMPLE 2: Out of the salary of Rs.123456, I kept 1/2 as savings. Out of the remaining money, I spend 47% on food and 18% on rent. How much do I spend on food and house rent?

Increase or Decrease Percent

To find the increase in percentage, work out the increase between the two numbers to be compared. Then, divide the increase by the original number and multiply the quotient by 100.

EXAMPLE 1: The population of a town in a particular year increased by 10%. Next year it decreased by 10%. Find the net increase or decrease percent in the initial population.

SOLUTION: Let the initial population of the town be x.
Population increased by= 10% X x= 0.1 X x =0.1x
Increase Population= (x+0.1x)= 1.1x
Next year, population decreased by= 10% X 1.1x= 0.1 X 1.1x= 0.11x
Decreased population= 1.1x- 0.11x= 0.99x
0.99x

Hence, I should reduce my consumption by 10.7% if the price of onions has increased by 12%.

Finding Discounts

Convert the percentage discount to a decimal.

• Subtract the discount from the original price
  
  For example,
  Discounted price for the shoes= Rs.(3456-414.72)
  =Rs. 3041.28

EXAMPLE 1: An item marked at Rs.1234 is sold for Rs.567. What is the discount and discount%?

SOLUTION: Discount Amount= Rs.(1234 – 567)= Rs. 667
Percentage Discount= (Discount Amount)/(Marked Price) X 100
=667/1234 X 100
=54.05%

Hence, Discount= Rs.667; Percentage Discount= 54.05% [ANS]

EXAMPLE 2: The list price of a dress is Rs.8901. A discount of 23% is announced on sales. What are the amount of discount on it and its sales price?

SOLUTION: Amount of discount= 23% X Rs.8901= Rs.2047.23
Sales Price= Rs.[8901- 2047.23] =Rs.6853.77

Hence, discount amount= Rs2047.23; sales price=Rs.6853.77. [Ans]

Profit & Loss

EXAMPLE 1: Arya sold two digital cameras at Rs. 30,000 each. On one she gains 12% and on the other, she loses 12%. What percent does she gain/loss on the transaction?

SOLUTION: For the first digital camera: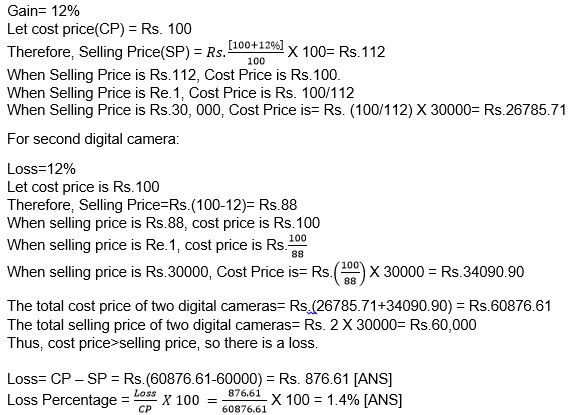

Hence, Arya loses 1.4% on the whole transaction.

Alternative Method:
If two commodities are sold at the same price and the seller gets the same amount of gain & loss on each commodity then the seller always incurs a loss on the whole transaction.

• Value Added Tax (VAT) is a tax on the value added at each transfer of goods, from the original manufacturer to the retailer.
  
  For example,
  Assuming the rate of tax is 12% and a person purchases an article for Rs.345.
  The tax he pays= Rs.(12% X 345) = Rs. 41.4
  Now, if he sells the same article for Rs. 678
  The tax he recovers= Rs.(12% X 678) = Rs. 81.36
  VAT = Tax recovered on the sale – Tax he paid on the purchase
  = Rs.(81.36 – 41.4) = Rs.39.96

EXAMPLE 1: Swathi bought the following articles from a departmental store

Calculate the total bill paid, including sales tax paid by Swathi to the departmental store.

SOLUTION: Cost price of 3 dress= Rs.1234 X 3 = Rs.3702
Sales tax on dresses = Rs. (12% X 3702) = Rs. 444.24
Amount paid for 3 dresses = Rs(3702+444.24) = Rs 4146.24

Cost price of 2 bags= Rs 567 X 2 = Rs 1134
Sales Tax on 2 bags = Rs (3% X 1134) = Rs 34.02
Amount paid for 2 bags = Rs(34.02+1134) = Rs1168.02

Cost Price of 1 Laptop = Rs89012
Sales Tax on Laptop = Rs. (4% X 89012) = Rs.3560.48
Amount paid for 1 laptop = Rs. (89012 + 3560.48) = Rs.92572.48

Cost Price of 2 dinner set = Rs. (2 X 345) = Rs. 690
Sales Tax on 2 dinner sets= Rs(5% X 690) = Rs.34.5
Amount paid for 2 dinner sets = Rs.(34.5+690) = 724.5

Hence, total amount of bill = Rs.[4146.24+1168.02+92572.48+724.5) = Rs.98611.24 [ANS]

EXAMPLE 2: A shopkeeper bought an AC at a discount of 12% from the wholesaler, the printed of the AC is Rs.34567. The shopkeeper sells it to a consumer at a discount of 8% on the printed price. If the rate of sales tax is 9%, find i) the VAT paid by the shopkeeper.
ii) the total amount that the consumer pays for the AC.

SOLUTION: M.P. = Rs.34567
Discount= 12% for shop-owner
Discount = 8% for consumer
Sales Tax = 9%

Discount for shopkeeper = Rs.(12% X 34567) = Rs. 4148.04
Cost for Shopkeeper = Rs(34567 – 4148.04) = Rs. 30418.96

Cost for Consumer = Rs(34567 – (8% X 34567)) = Rs. 31801.64

31801. Tax charged by the shopkeeper= Rs.(9% X 31801.64) = Rs. 2862.1476
       Tax paid by the shopkeeper = Rs.(9% X 30418.96) = Rs.2737.7064
       Hence, VAT paid by the shopkeeper = Rs.(2862.1476 – 2737.7064) = Rs. 124.44

31801. Amount paid by the consumer = Rs.(31801.64 +2862.1476) = Rs. 34663.78[Ans]

Compound Interest

• 

  

  Practice these questions

  Q1) The ratio of a number of boys and number of girls in a school of 1234 students is 5:6. If 78 new boys are admitted, find how many new girls should be admitted to make the ratio 1:2.

  Q2) Rachel gets 91 marks in her exam. These are 23% of total marks. Find the Maximum number of marks.

  Q3) Increase 123 by 4% and then decrease it by 5%. Find the final number.

  Q4) The marked price of a water cooler is Rs. 14650. The shopkeeper offers an off-season discount of 8% on it. Find its selling price.

  Q5) Monica bought 2 dozen eggs for Rs. 156. Since 7 of them broke, he incurred a loss of Rs.120 on selling them. What was the selling price of one egg?

  Q6) A manufacturer printed the price of his goods as Rs.1120 per article. He allowed a discount of 4% to the wholesaler who in his turn allowed a discount of 3% on the printed price to the retailer. If the prescribed rate of sales tax on the goods is 5% and the retailer sells it to the consumer at the printed price then find the value-added tax paid by the wholesaler and the retailer.

  Q7) Vivan took a loan of Rs. 654987 from the bank. If the company charges interest at 15% per annum, compounded quarterly, what amount will discharge his debt after one year?

  Recap

  • Percentage is not cumulative in nature.
  • Sales taxis collected by the retailer when the final sale in the supply chain is reached via a sale to the end consumer.
  • Compound Interest is the interest calculated on the initial principle and also on the accumulated interest of previous periods of a deposit or loan.