Real Numbers

What are real numbers? Why numbers have been called real here? Before starting try to answer this question. We all have been studying numbers from class 1 or even before that, and hence we all know such a huge variety of numbers which can be in million or trillions or any number. But here let me ask you how do we categorise them and basically on which basis they have been classified. So let’s find some interesting answers to these interesting questions.

Any number which can be represented on a number line is called a real number. Here the numbers are called real because we use and apply these numbers in our real world and they are equally related to the real world entities.

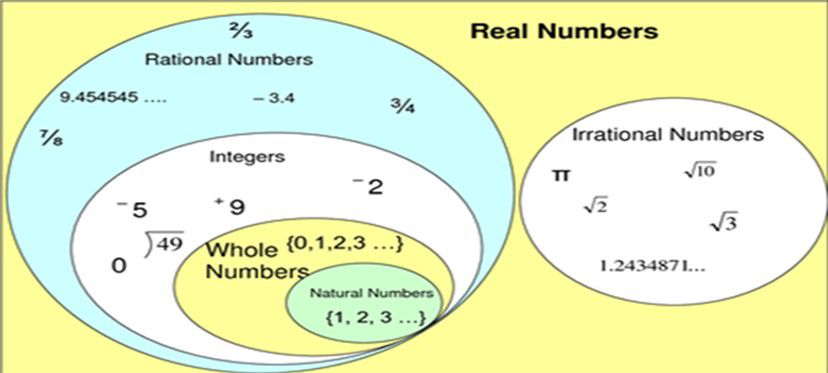
If we consider Real number as a set then rational numbers and irrational numbers are its subsets and integers, whole numbers and natural numbers are further the subsets of rational number.

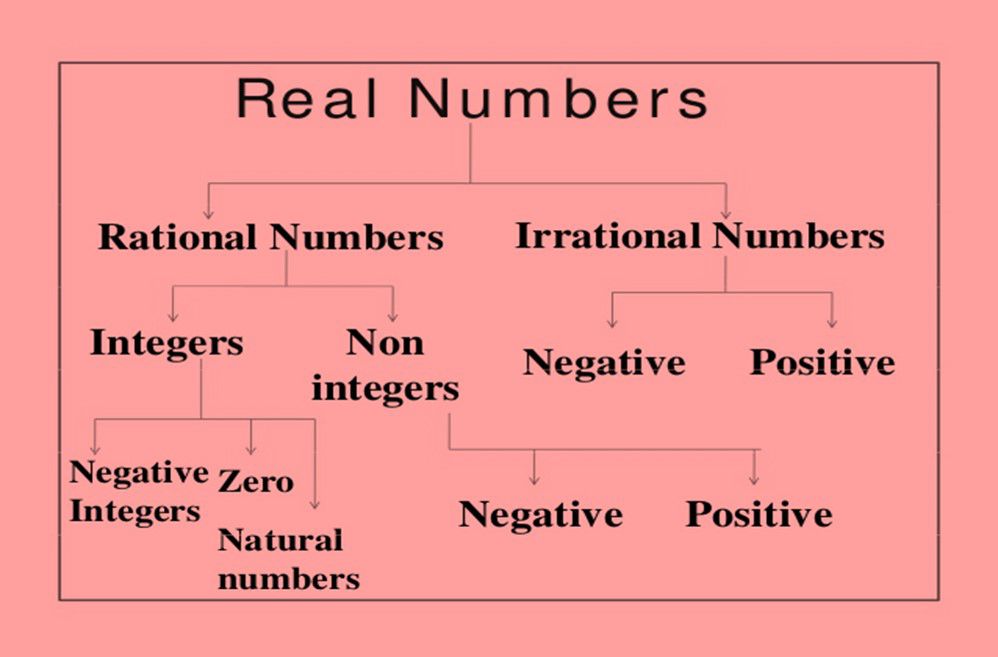
Real numbers have been classified in two basic categories and these two categories are further classified in sub categories. Let’s go through a flow chart described below:

Rational numbers

The numbers which can be represented in the form of p/q where p and q are integers and q≠0 is called as rational number.

Example 1: 2/3, 4/9, 8/7, 11/10, etc.

Here an important point is to remember that p and q must be co-prime numbers.

Rational numbers are further classified into two categories:

1. Integers: An integer is any number which can be written without any fractional part. For example 3,-2,56 are integers because they doesn’t have any fractional part.

• Integers are further classified as:
• Whole Numbers: Integers starting from 0 are called as whole numbers.
• Natural Numbers: Integers starting from 1 are called as natural numbers.

1. Non Integers: Those numbers which are not integers that is they actually are fractions are called non integers. For example 2/7, 3/5 etc are fractions.

• Non Integers can be positive like 7/4, 8/9 etc. and can also be negative like -7/4 or -8/9 etc.

Irrational Numbers

The numbers which cannot be written in the form of p/q are called as irrational numbers. Example √2, √3 etc.

• Here a question arises √2 can be represented as √2/1 even then it is irrational. Why?
• It has a very simple answer which hides in the definition of rational numbers. There was mentioned that in p/q, p and q both must be integers and here √2 is strictly not an integer.

Properties

Rational as well as irrational number have certain identities as well as certain properties:

Let R1 and R2 be two rational numbers and S1 and S2 be two irrational numbers:

1. R1 x R2 or R1÷R2 will always be rational number.

Example 2: Let 2/7 and 4 be two rational nos. Show that their product and division is also rational.

Solution: Product = 2/7 x 4/1 = 8/7. (Rational number)

Division = 2/7 ÷ 4/1 = 2/7 x 1/4 = 1/14. (Rational number)

1. R1±R2 will always be a rational number.

Example 3: Let 7/2 and 5/2 be two rational nos. Show that their addition and subtraction both results a rational number.

Solution: Addition = 7/2 + 5/2 = 12/2 = 6 (Rational Number).

Subtraction = 7/2 – 5/2 = 2/2 = 1 (Rational Number).

1. R ±S will always be irrational.

Example 4: Let 4 and √4 are rational and irrational nos. Show that their addition and subtraction results in an irrational number.

Solution: Addition = 4+√4 (Irrational number).

Subtraction = 4-√4 (Irrational number).

1. R x S or R÷S will always be irrational.

Example 5: Let 2 and √2 be a rational and an irrational no. Show that their product and division results in an irrational number.

Solution: Product = 2 x √2 = 2√2 (Irrational number).

Division = 2/√2 and after rationalizing we get √2

(Irrational number).

1. S1±S2 will always be irrational.

Example 6: Let √3 and √5 be two irrational nos. Show that their addition and subtraction results in an irrational no.

Solution: Addition = √3+√5 (Irrational Number).

Subtraction = √3-√5 (Irrational number).

1. S1 x S2 or S1÷S2 can be rational or can be irrational.

Example 7: Let √3 and 4√3 be two irrational numbers. Find their product and division.

Solution: Product = √3 x 4√3 = 4 x 3 = 12. (Rational Number)

Division = 4√3 ÷ √3 = 4 (Rational Number)

Example 8: Let √5 and √3 be two irrational numbers. Find their product and division.

Solution: Product = √5 x √3 = √15 (Irrational Number)

Division = √5 ÷ √3 = √(5/3) (Irrational number).

Properties of Real Numbers

Practice Questions

Q1) what are the differences between Rational and Irrational numbers.

Q2) State True or False:

1. All natural numbers are whole numbers.
2. All whole numbers are natural numbers.
3. All integers are rational numbers.
4. All rational numbers are integers.
5. Fractions are non-integers.

Q3) What will be the product of √2 and √5. Is it rational or irrational?

Recap

• All the numbers which can be represented on a number line are real numbers.
• Integers are those rational numbers where the denominator is 1.
• All integers are rational numbers but vice versa is not true.
• All natural numbers are whole numbers but vice versa is not true.
• Real numbers show commutative associative and distributive properties.