Fractions

 Fractions         

We all have heard of this word in the field of mathematics as well as in our everyday lives. For example when we divide a chocolate in two pieces, it is a fraction. When we eat half of an apple it’s a fraction. In mathematics fraction plays a very important role and let’s find out how?

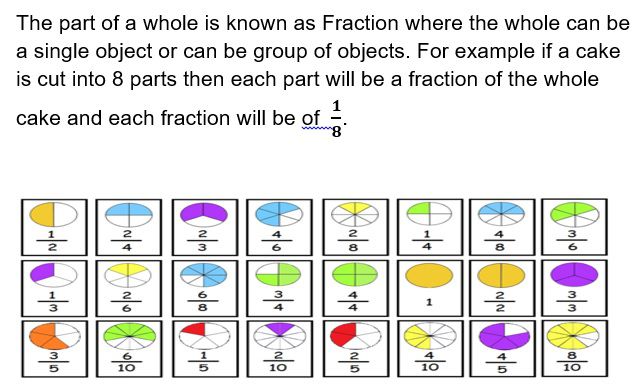
Understanding Fractions

A fraction consists of two parts:

1. Numerator: The part which is written above the horizontal line is called as numerator.
2. Denominator: The part which is written below the sleeping line horizontal line is called as denominator.

Thus a number is written above and a below the horizontal line and then the arrangement is called as fraction.

Types of Fractions

There are three types of fractions

1. Proper Fraction: - Fraction whose numerator is less than the denominator is called a proper fraction.

Example 2: 1/4, 5/8, 3/5, 4/7, etc.

2. Improper Fraction: Fraction whose numerator is either equal or greater than the denominator.

Example 3: 5/2, 7/4, 9/7, 13/11, 2/2, etc.

3. Mixed Fraction: - A combination of a whole number and fraction together is called mixed fraction.

Example 4: Convert the fraction 17/4 in mixed fraction.

Example 5: Solve the above example.

Solution: To solve this we will follow 3 steps

• Multiply the whole no. with denominator. (2 x 3 = 6).

• Add the answer obtained in step 1 to the numerator

(6 +1 = 7).

• Place the result obtained in step 2 in the place of numerator and the denominator remains the same.

Hence the fraction becomes 7/3 which is an improper fraction.

There is another category of fractions called as

Equivalent Fractions: Those fractions which look different but on solving become same.

• To find an equivalent fraction of a given fraction, you may multiply both the numerator and the denominator of the given fraction by the same number.

• To find an equivalent fraction, we may divide both the numerator and the denominator by the same number.

• A fraction is said to be in the simplest (or lowest) form if its numerator and denominator have no common factor except 1 and HCF helps us to reduce a fraction to its lowest form.

Like and Unlike Fractions

Fractions with same denominators are called like fractions. For example 2/3, 4/3, 5/3 etc are all like fractions.

Fractions which don’t have same denominators are called as Unlike Fractions. For example, 2/5, 4/7, ½, etc. is unlike fractions

Comparing Fractions

Comparing means to find out some characteristics like which one is smaller and which is greater when two or more numbers are observed together which means compared together.

Here we are going to compare two fractions whose denominators are same that is they are like fractions.

Now observe the numerator, the fraction whose numerator is greater will be the greater fraction.

Example 7: Compare who is greater 6/7 or 5/7.

Solution: Here both the fractions have the same denominator and hence on observing the numerators we get that 6 is greater than 5 there 6/7 is greater than 5/7.

6/7 > 5/7

When we have to compare two fractions which don’t have same denominators that is they are unlike fractions then we will compare them in the following manner:

1. a) Check if the numerator is same or not, if yes then the fraction with the lower value of denominator will be greater.
2. b) If the numerator is not same then try to make the either the numerator or denominator of both the fractions same then use the previous steps.

Computing operations on fractions

As we all know that addition, subtraction, multiplication and division are the computing operations.

Here we are going to study only the first two computation operations on fractions.

Addition and Subtraction of Fractions

Two fractions with the same denominator can be added or subtracted by using the two steps:

• Observe that the denominators of both the fractions are same.
• Add or subtract the numerators as asked in the questions.

Example 8: Add and subtract 4/5 and 3/5.

Solution: As we can see the denominators of both the fractions is same and hence we can add and subtract them by using the numerators.

Therefore, 4/5 + 3/5 = 7/5 and 4/5 – 3/5 = 1/5.

• When the denominators are different then we will take the LCM of the denominators to make the denominators same and multiply the same factor with numerator and then add or subtract the numerators as asked in the question.

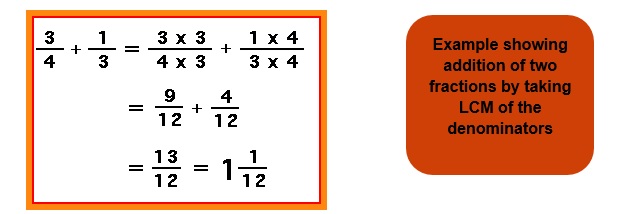
Practice Questions

Question 1: Write the natural numbers from 102 to 113. What fraction of them are prime numbers?

Question 2: Which one is smaller 1/13 or 13/13?

Question 3: Solve the mixed fraction 5 ½.

Question 4: State True or False:

4. 3/4 > 1/4.
5. 5/9 = 10/18.
6. 12/13 < 9/13.
7. 13 /11 is an improper fraction.
8. 11/11 is a proper fraction.
9. 15/17 is a proper fraction.

Question 6: Compute the answers of the following:

1. 4/3 + 5/2 = ?
2. 17/12 – 15/6 = ?
3. 5/2 + 1/4 = ?

Recap

• The part of a whole is fraction.
• Numerator and denominator are the parts of a fraction.
• Fractions can only contain integers
• If denominators are same then we can compare the fractions by comparing the numerators.
• If Numerator > or = Denominator then improper fraction.
• If Numerator < Denominator then proper fraction.
• A fraction is said to be in the simplest (or lowest) form if its numerator and the denominator have no common factor except 1.