• A decimal is a fraction whose denominator is a power of ten and whose numerator is expressed by figures placed to the right of a decimal point.

For example, 123.45 is a decimal number. The digits to the left of the point are an integral part or whole number part and digits to the right of the point are decimal part or fractional part.

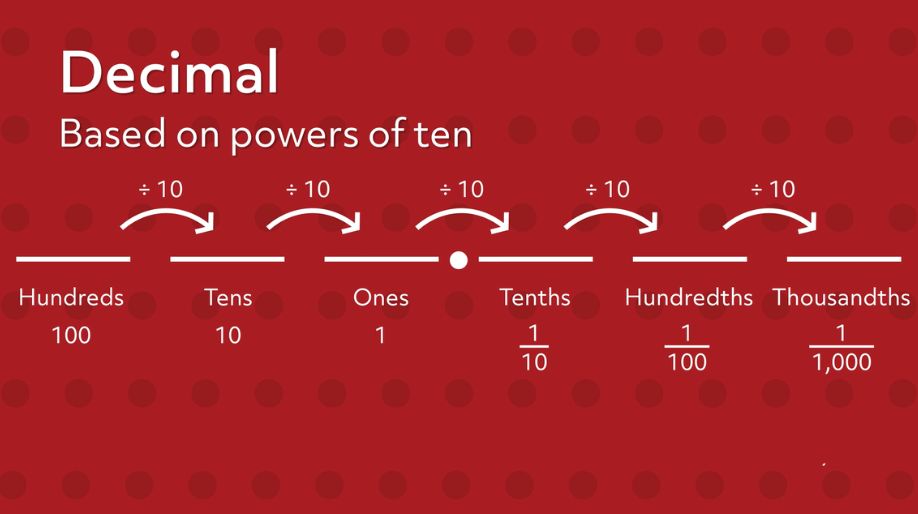
• Given below is how we write the decimal number on the place value chart:

Converting Fractions With 10, 100 As Denominators into Decimals

STEP 1: Consider the fraction and

STEP 2: Now, write 3 in tenths () place for . And write 4 at hundredths place for .

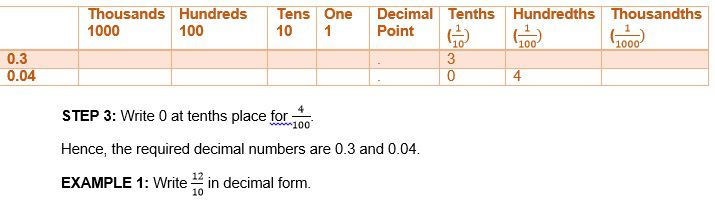
SOLUTION: The last digit in the numerator (2) will be written in tenths place as the number 12 is divided by 10.

In the place value chart, numbers are written from the right side to left. Because of this the number 1 will be written left of the decimal point.

SOLUTION: The last digit in the numerator, 3, will be written in hundredths place as the number, 123, is divided by 100.
The direction of writing the number in the place value chart is from right to left. Because of this 2 will be written at tenths place and 1 will be written at one’s place.

EXAMPLE 1: Convert 1.03 into a fraction.

SOLUTION: The number of digits in the decimal part is 2. [ Count 0 as a significant digit if it
is in between decimal point and
the lowest place value.]

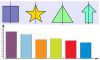
Write a fraction and decimal number equivalent for the shaded portion.

EXAMPLE 2: Convert 012.340 into a fraction.

SOLUTION:

Don’t Count 0 as a significant digit:
i) If it is placed left of the highest place value.
ii) If it is placed right of the lowest place value after the decimal point.

Like and unlike decimals

• Decimals having the same number of decimal places are called like decimals.
  
  For example,
  23, 2.34, 3.45
  each has 2 decimal
  places. Hence, these are
  like decimals.
• Decimals not having the same number of decimal places are called, unlike
  
  For example,
  1.2, 2.34, 3.456
  each has decimal
  places 1, 2, and 3 respectively.
  Decimal places are not same. Hence,
  these are unlike decimals.
  EXAMPLE 1: Convert 6.7, 7.89, 8.901 to like decimals.
  
  SOLUTION: 6.7 has 1 decimal place.
  7.89 has 2 decimal places.
  8.901 has 3 decimal places.
  The highest number of decimal place is 3.
  Hence, we have to put two 0 in 6.7 to make it 3 decimal places. And
  one 0 in 7.89 to make it three decimal places. Now, the numbers are 6.700, 7.890, and 8.901 and these 3 are like decimals.

Ordering of decimals

• Decimals can be arranged in ascending order and descending order. In ascending order, the smallest number is placed first and largest number is placed last. In descending order, the largest number is placed first and smallest number is placed last.

EXAMPLE 1: Arrange the three decimal numbers 1.203, 1.23, and 0.5 in ascending order.

SOLUTION: In a table, they look like this:

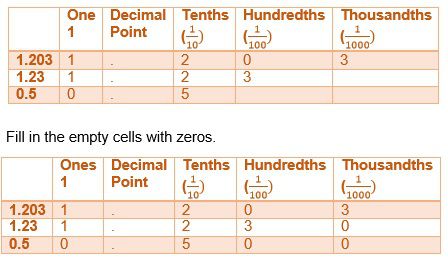
Compare using the first column(Ones)
Two of them are 1 while the last one is 0. Ascending order needs smallest first. Hence, 0.5 is taken out.

• Now the table looks like:

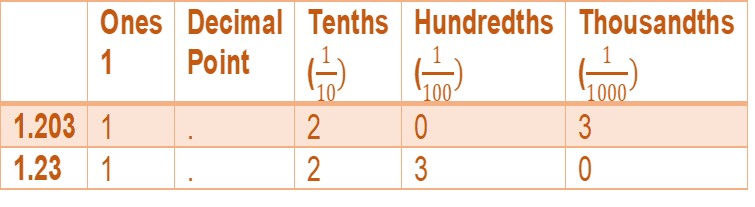
• The tenths value, 2, is same for both the numbers. So, we will move to hundredth’s place. One number has 0 in hundredth while the other has 6. 0<6, so the next smallest number is 1.203
• Hence, the numbers in ascending order are5, 1.203, 1.23. [ANS]

EXAMPLE 2: Arrange the number 1.24, 0.35, 67.891 in descending order.

SOLUTION: In a place value chart, the numbers look like this:

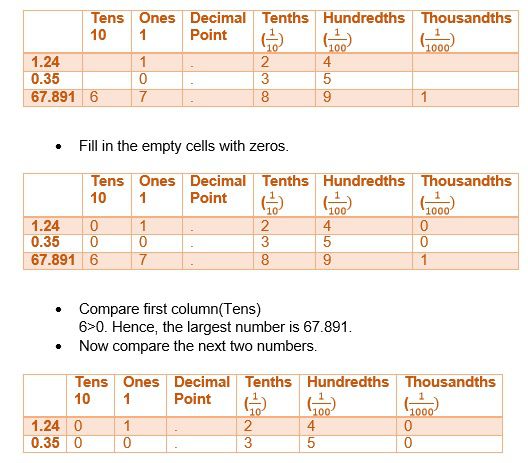
• Compare the next column(Ones).
  1>0. Hence, the next largest number is 1.240.
• Thus, the numbers in descending order are 67.891>1.24>0.35>. [ANS]

Addition and subtraction of decimal

• To add decimal numbers, insert zeros in empty decimal place values so that all of the numbers will have same decimal places.
  
  For example,
  2+2.34+8 will
  be written as 1.20+2.34+8.00
• To subtract a small decimal number from a larger decimal number, write them down with the larger one on top and the decimal points underneath one another. Then calculate the subtraction as you would for whole numbers.

EXAMPLE 1: Add 1.2 + 34.56 + 789.012

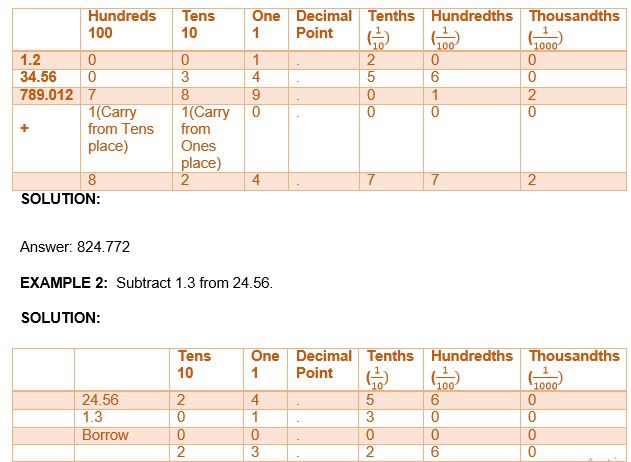
Answer: 23.26

Multiplication of a decimal number by a whole number

• Each time we multiply a decimal number by a power of 10, the decimal point is moved one place to the right.
  
  For example, see the following table:

• The total decimal digits in the multiplicand and multiplier should be equal to the decimal digits in the product.
  For example,
  2 X 2 = 2.4 (1 decimal digit)
  1
  decimal
  digit)

EXAMPLE 1: An electrician earns Rs.12.34 per hour. If he worked 256 hours this month, then how much did he earn?

SOLUTION:

Money earned by the electrician=Rs. (12.34 X 256)

Hence, the electricians earned Rs.3130.88 for 256 hours of work. [ANS]

EXAMPLE 2: Which is greater: 12.3 X 40 or 123 X 4?

SOLUTION: 12.3 X 40 = 12.3 X (10 X 4) = (12.3 X 10) X 4 = 123 X 4 Hence, 12.3 X 40 and 123 X 4 are both equal.

Division of a decimal number by 10, 100, 1000

• The common way to divide decimals by powers of ten is to move the decimal point left as many steps as there are zeros in the number 10, 100, 1000 etc.

Multiplication of a decimal number by a decimal number

Hence, 6.78 X 9.01 = 61.0878 [ANS]

Division of a decimal number by whole number & another decimal number

EXAMPLE 1: Divide the decimal number 23.45 by the whole number 5.

SOLUTION:

The quotient is 469. But, we had to put 0 twice to make the remainder divisible by 500.
Hence, put a decimal point 2 places from the lowest place value. [0 twice so 2 decimal
places]

Therefore, the quotient is 4.69. [ANS]

EXAMPLE 2: Divide the decimal number 67.85 by another decimal number 2.5.

SOLUTION:

-1750
350 [Put 0]
-250
1000 [Put 0]
-1000
0000

The quotient is 2714. But, we added 0 twice. Because of this we have to put a decimal point
2 places left of the lowest place value. Hence, the answer is 27.14.

Converting a fractional number into decimal number

STEP 3: Write down 4 with decimal point 1 space from the right. (because 10 has 1 zero)

Answer= 0.4

EXAMPLE 2: Convert 16/3 into a decimal number.

SOLUTION:

STEP 1: There is no way to make 3 a multiple of 10, 100, or any 1 followed by any no. of zeros.

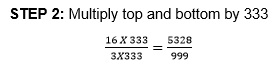
STEP 3: Now, 999 is nearly 1000, so let us write down 5333 with decimal point 3 spaces from the right. (Because 1000 has 3 zeros)

Answer: 5.333 [Approx.]

Practice these questions

Q1) Convert the following decimal numbers into mixed fractions:
i)1.2 ii)23.45 iii)678.901

Q2) Arrange the decimal numbers in ascending order:
i)2.3, 1.34, 32.57, 0.89
ii) 1.23, 4.45, 6.35, 2.46, 2.57, 2.45
iii)2.45,3.46,2.32,1.23,7.78,2.34

Q3) Arrange the decimal numbers in descending order:
i)2.31,2.42,67.6,5.6,2
ii)2.08,7.89,7.98,9.87,2.34,3.42
iii)1.23,5.43,8.76,2.32,7.76

Q4) Add the following numbers:
i)1.2+3.4 ii)56.78+90.12 iii)345.678+901.234

Q5) Subtract the following numbers:
i)5.6-3.4 ii) 78.901- 23.456 iii)234.567-56.789

Q6) Multiply the following numbers:
i) ii) 45.67 X 89.01 iii) 234.567 X 890.123

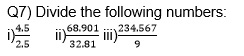
Q8) Subtract one and two-tenths from eleven and eighty-one hundredths.

Q9) If you ran 1km on Monday, 23.45 hm on Tuesday, 678.901 metres on Wednesday, how many Kilometres did you run, total, for three days?

Q10) If you divide Rs.2345.6785 among 5 children, how much would each child get?

Recap

• Decimal numbers having equal number of decimal places are called like decimals.
• Decimal numbers having unequal number of decimal places are called unlike
• In XX.YY, the integral part is XX and the decimal part is YY
• While performing addition or subtraction always line up the decimal point.
• While performing multiplication of decimal numbers, the number of decimal places in the product should be equal to the total decimal places in the multiplicand and multiplier.
• While performing division of decimal numbers, the total number of 0s added after the lowest place value should be equal to the decimal places in the quotient.