If we look anywhere we will easily find the numbers around us. Your age, your class, your height each and every thing is related to the numbers. Isn’t this beautiful? Let’s learn more about the beauty of numbers and mathematics.
Comparing Numbers
Numbers can be compared whether they are large or small on the basis of their thousands, then hundreds, tens and even ones.
For example we can compare 2021 and 200 that 2021 is larger number because of its thousand values.
When we have to arrange objects according to some criteria, it can be done in two ways:
1) Ascending order: Ascending order means arrangement from the smallest to the greatest.
2) Descending order: Descending order means arrangement from the greatest to the smallest.
Example 1: Arrange the numbers in descending order- 8754, 56, 9852, 124, 652.
Solution: In descending order we will start from largest number and end up in smallest hence the order will be
9852, 8754, 652, 124, 56.
On adding 1 to the largest two digit number we get the smallest three digit number. The same phenomenon is with all 3,4,5 digit numbers.
It means 99,999 is largest 5 digit number hence on adding 1 we get 1,00,000 smallest 6 digit number called lakh.
Revision of Place Values
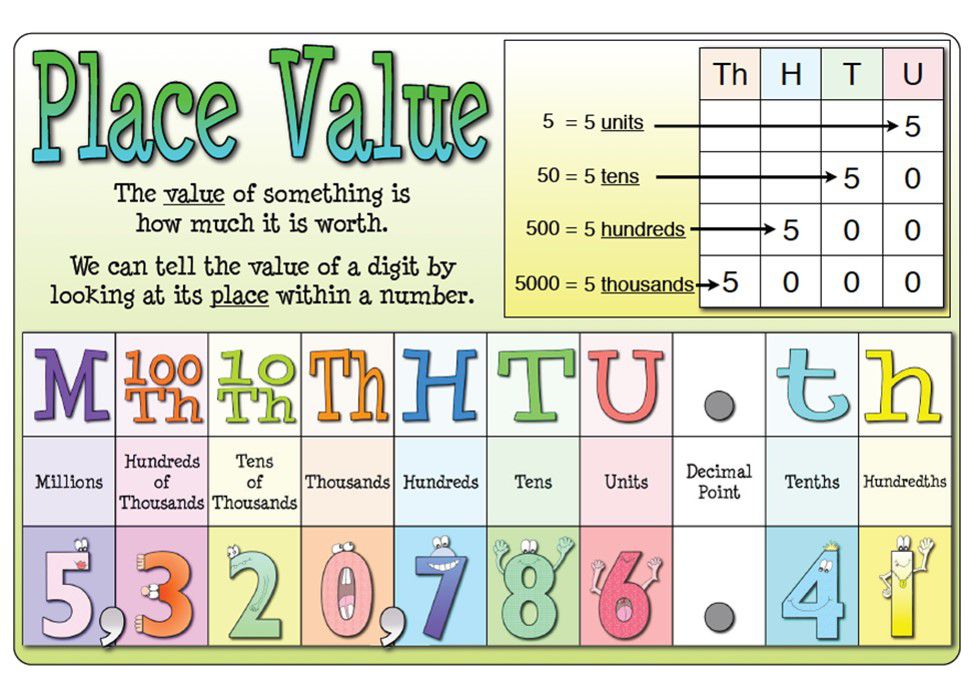
Estimation
In estimation we try to get close to the answer as much as possible by predicting all the possibilities. We make a rough idea about the case or condition.
Example 1: Find the value of 63 x 987.
Solution: Since it is very difficult to find the product of such large numbers, therefore we are going to use estimation here.
We can say that 63 is close to 60 and 987 is close to 1000 and hence the product 63 x 987 will be close to 60 x 1000
And hence the value of 63 x 987 is close to 60,000.
Using Brackets
Sometimes we all come across some big mathematical expressions and to calculate the value we have to be very precise. Hence to solve such big mathematical expressions very easily we use brackets.
An important about brackets is to be remembered that they are solved first in any expression that is the expression written inside the bracket will be solved first.
Example 2: Solve 17 x 109.
Solution: Solving such a big number’s multiplication is not very easy hence we will use brackets here
We can write 17 x 109 as
17 x 109 = (10+7) x 109
= 10 x 109 + 7 x 109
= 10 x (100+9) + 7 x (100 + 9)
= 10 x 100 + 10 x 9 + 7 x 100 + 7 x 9
= 1000 + 90 + 700 + 63
= 1,853.
Roman Numerals
The numbers from 0 – 9 and also their magical combinations can also represented using certain alphabets and this representation is called Roman Numerals.

Example 3: Write the roman numeral of 54.
Solution: Here we will use the brackets that is, we can write 54 as (50+4) = (L + V) = LV
Whole Numbers
- The number starting from 0 are called as whole numbers.
- The numbers staring from 1 are called as natural numbers.
- The successor of any number is next number that is +1 and predecessor is the previous number that is -1.
Properties
Whole numbers follows some properties which are:
- a) Addition and Multiplication are commutative for whole numbers. It means that if two whole numbers a and b are added and multiplied then,
a + b = b + a and a x b = b x a.
- b) ) Addition and Multiplication are associative for whole numbers. It means that if a, b and c are any three whole numbers then
a + (b + c) = (a + b) + c and a x ( b x c) = (a x b) x c.
Example 4: Find the value of 4 x 25 x 564.
Solution: It is very difficult to find the product of such a large number hence we will use the property of associativity which means
4 x 25 x 564 = (4 x 25) x 564
= 100 x 564 = 56400.
Factor and Multiples
A factor of a number is an exact divisor of that number. For example factor of 12 is 1, 2, 3, 4, 6 and 12 itself are the factors of 12.
- 1 and the number itself are always the factors of the number.
- Every factor is always less than or equal to the number.
A number that may be divided by another a certain number of times without a remainder. For example, the multiple of 12 is 24, 48, 60 etc.
- Every multiple of a number is greater than or equal to that number.
- Every multiple of a number is greater than or equal to that number.
- Every number is a multiple of itself.
A number for which sum of all its factors is equal to twice the number is called a perfect number. The numbers 6 and 28 are perfect numbers.
Example 5: Find the factors and multiples of 45.
Solution: 45 = 1 x 45 45 = 3 x 15
45 = 5 x 9
Hence the factors are 1, 3, 5, 9, 15 , 45 .
Multiples will be 45, 90 , 135, 180 etc.
Prime and Composite Numbers
The numbers other than 1 whose only factors are 1 and the number itself are called Prime numbers.
Numbers having more than two factors are called composite numbers.
The numbers which are a multiple of 2 are called as even numbers. And the numbers which aren’t are called as odd numbers.
- 2 is the only even prime number and also the smallest prime number.
Divisibility Test
Divisibility by 2: A number is divisible by 2 if it has any of the digits 0, 2, 4, 6 or 8 in its ones place.
Divisibility by 3: If the sum of the digits is a multiple of 3, then the number is divisible by 3.
Divisibility by 4: A number with 3 or more digits is divisible by 4 if the number formed by its last two digits (i.e. ones and tens) is divisible by 4.
Divisibility by 5: A number which has either 0 or 5 in its ones
place is divisible by 5.
Divisibility by 6: If a number is divisible by 2 and 3 both then it is divisible by 6 also.
Divisibility by 8: A number with 4 or more digits is divisible by 8, if the number formed by the last three digits is divisible by 8.
Divisibility by 9: If the sum of the digits of a number is divisible by 9, then the number itself is divisible by 9.
Divisibility by 10: if a number has 0 in the ones place then it is divisible by 10.
Divisibility by 11: find the difference between the sum of the digits at odd places (from the right) and the sum of the digits at even places (from the right) of the number. If the difference is either 0 or divisible by 11, then the number is
divisible by 11.
Example 6: Find whether the number 52749 is divisible by 9 or not ?
Solution: As we know that to check whether the number is divisible by 9 or not we must add the digits of the number.
Therefore on adding we get,
5 + 2 + 7 + 4 + 9 = 27
Since the number 27 is divisible by 9 hence the number 52749 is also divisible by 9.
Highest Common Factor (HCF) and Lowest Common Multiple (LCM)
The Highest Common Factor (HCF) of two or more given numbers is the highest (or greatest) of their common factors.
The Lowest Common Multiple (LCM) of two or more given numbers is the lowest (or smallest or least) of their common multiples.
Prime Factorization
When any number is written in the form of its factors, it is said to be factorized. And when the same number is factorized in terms of only prime numbers we call it prime factorization.
Example 7: Find the prime factorization of 56 and 28 and hence find out the HCF.
Solution: The prime factorization of 56 = 2 x 2 x 2 x 7.
And the prime factorization of 28 = 2 x 2 x 7.
The HCF can be easily seen as 2 x 2 = 4.
Example 8: Find the LCM of 20, 25 and 30.
Solution: The prime factorization of 20 = 2 x 2 x 5.
The prime factorization of 25 = 5 x 5.
The prime factorization of 30 = 2 x 3 x 5.
Here the prime number 2 appears for maximum 2 times, 3 for maximum 1 time, 5 for maximum 2 times.
Hence the LCM will be = (2 x 2) x 3 x (5 x 5) = 300.

Practice Questions
Q1) Arrange the numbers in increasing order 254, 87, 562 , 32564, 4581, 98778, 45, 12365, 456217.
Q2) Find the estimate product of 206 x 789.
Q3) Find the value of 27 x 104.
Q4) Write the following numbers in Roman numeral:
45,12, 32, 89 ,100.
Q5) Write the predecessor and successor of the following number: 1236, 789, 5474, 32658, 45789.
Q6) Check whether the number 12560 is divisible by 5 and 10 or not ?
Q7) Check whether the number 45847 is divisible by 6 and 9 or not ?
Q8) Find the HCF and LCM of the following numbers:
45 and 60, 30 and 150, 25 and 100.
Recap
- A factor of a number is an exact divisor of that number every number is a factor of itself. 1 is a factor of every number.
- Every number is a multiple of each of its factors every multiple of a given number is greater than or equal to that number every number is a multiple of itself.
- Commutativity, Associativity and Distributivity properties of whole numbers are useful in simplifying calculations and we use them without being aware of them.
- Zero is the identity for addition of whole numbers. The whole number 1 is the identity for multiplication of whole numbers.
- All natural numbers are whole numbers, but all whole numbers are not natural numbers.
- Every whole number has a successor. Every whole number except zero has a predecessor and every natural number has a successor. Every natural number except 1 has predecessor.
- We use the Hindu-Arabic system of numerals. Another system of writing numerals is Roman Numerals.