We all come across many equations in which some contains one or two or three variables. And for solving these equations we require exactly the same number of different equations according to the number of variables. But here an important point is to be noticed that the equations must be linear but, why? Let’s try to find out the answer to such questions.  

The pair of two equations containing only two variables and each term has degree 1 is called a pair of linear equations in two variables.  For example, 4x+2y=7 and 3x-2y=7 is a pair of linear equation in two variables x andy.

On solving the two equations we get values of x and y which are called as the solutions of these equations.

The general form of a pair of linear equations in two variables is

a1x + b1y = c1

a2x + b2y = c2 

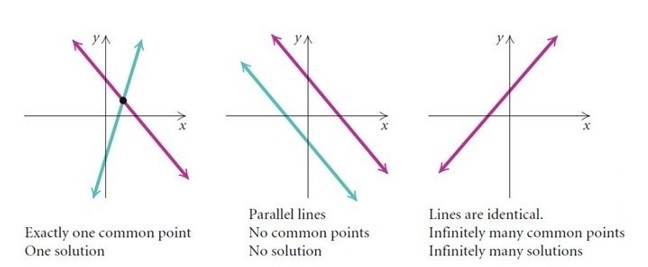
Since these two equations are of degree one and hence they will represent two straight lines. Now when we try to represent these two straight lines in a Cartesian plane we have three conditions:

  1. a) These two lines intersect
  2. b) Two lines overlap each other
  3. c) These two lines are parallel

Maths class 10 Pair of Linear Equations in Two Variables                                        

Solutions of the Equations 

As discussed above on solving the linear equations we can find out the solutions and these solutions follow some basic rules which are:

  1. a) If the equations have no solution then they are called as an inconsistent pair of linear equations.
  2. b) If the equations possess any solution then they are called as the consistent pair of linear equations.

If a pair of a linear equation has infinitely many solutions then it is called as the dependent pair of linear equations and pretty obvious that it will be consistent also.

We can solve the pair of linear equations by two methods which are:

  1. a) By using Graphical method
  2. b) By using algebraic method

Graphical method is very easy but requires high precision as the graphs have to be made very carefully because as the graph changes the solutions as well as the coordinates of the intersecting point changes.

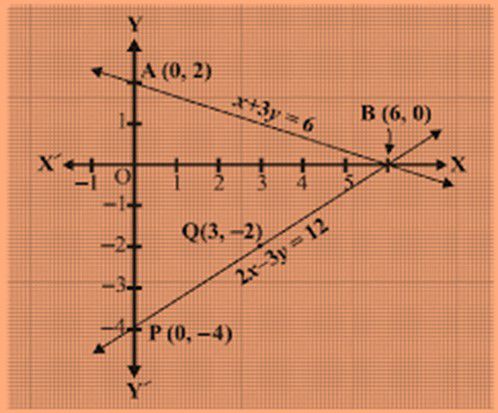
Example 1: Solve the pair of linear equation by using graph method x+3y=6 and 2x-3y=12.

Solution: We will plot the graph of the lines individually and then try to find out the intersection point.

Maths class 10 Pair of Linear Equations in Two Variables

 

An algebraic method includes certain methods which are:

  1. a) Substitution method: In this method, we are going to follow 3 steps to obtain the solution of the linear equation:

Example 2: Find the solution of the linear equations 4x+y=7 and x+y=4 by the substitution method.

Solution:

STEP 1:  Writing the value of any variable in terms of the other variable. For example, if any linear equation is 4x+y=7 then we can write it as y = 7-4x.

STEP 2:  Substitute the value obtained in step 1 in the second linear equation and obtain the value of the variable. For example, x+y=4 is the second linear equation then we can write it as:

 x+7-4x=4 which means -3x = -3 which means x=1.

STEP 3: Now by using the value obtained in step 2 find the value of the next variable.

Like here on putting the value of x in the 1st linear equation we get y= 7-4 = 3.

Hence the solution is x=1 and y=3.

  1. b) Elimination Method: In this method, we try to eliminate one variable by manipulating or multiplying both the equations with scalar constants then performing the arithmetic operations.

Example 3: Use elimination method to find the solution of the following equations:

2x+y=4 and x-3y=3.

Solution: Here we have equation 1 as 2x+y=4 and equation 2 as x-3y=3.

On multiplying the equation 1 by 3 we get equation 1 as

6x+3y = 12 as equation 3.

On adding both the equations we get

3x = 15 which means x = 5 and on putting this in equation 1 we get y = -6.

  1. c) Cross Multiplication Method: We can understand this method with the following 3 steps:

Let us consider a pair of linear equations in two variables

a1x+b1y=c1

a2x+b2y=c2

Step 1: we will multiply the 1st equation by b2 and 2nd by b1 that is by the coefficients of y.

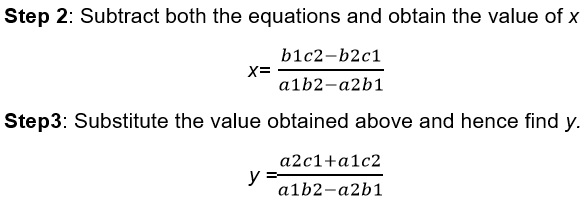
Maths class 10 Pair of Linear Equations in Two Variables

 

Here we can see that we have two cases

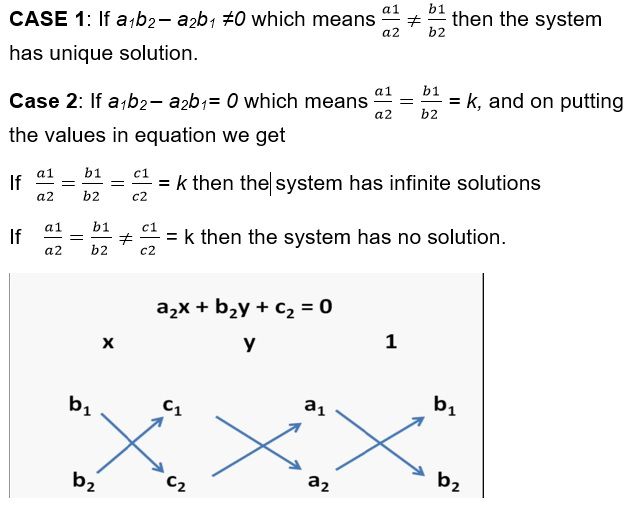
Maths class 10 Pair of Linear Equations in Two Variables

Equations Reducible to Linear equations

We all have to deal with a lot of real-life entities in which we will surely use this system of linear equations in two variables and it’s quite obvious that we are not going to get these equations as it is so let’s learn how to reduce equations to this form through an example:

Example 4: Solve the pair of linear equations:

2/x + 3/y = 13 and 5/x – 4/y= -2.

Solution: As it can be observed the equation is not of the form ax+by=c hence we have reduced it to its general form of linear equations:

Let us assume that 1/x = r and 1/y = s.

So the equation can be written as

2r+3s=13 and 5r-4s=-2

And on solving the equations by any of the above mentioned method we get,

r = 2 and s=3 which means 1/x= 2 and 1/y =3

which means x = 1/2 and y = 1/3.

Practice Questions

Q1) What is the degree of each term in a pair of linear equation in two variables?

Q2) The area of a rectangle gets reduced by 9 square units, if its length is reduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and the breadth by 2 units, the area increases by 67 square units. Find the dimensions of the rectangle.

 

Q3) A boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours, it can go 40 km upstream and 55 km downstream. Determine the speed of the stream and that of the boat in still water.

Recap

  • The pair of two equations containing only two variables and each term has degree 1 is called a pair of linear equations in two variables.

Maths class 10 Pair of Linear Equations in Two Variables

 

 

  • We can solve linear equation in two variables algebraically by using three methods which are
  1. a) Substitution Method
  2. b) Elimination Method
  3. c) Cross Multiplication method