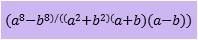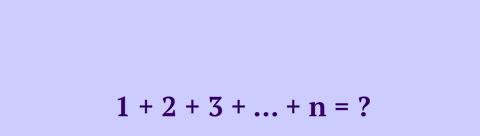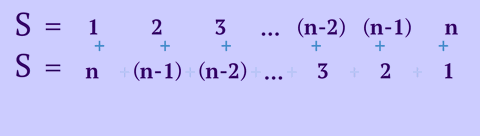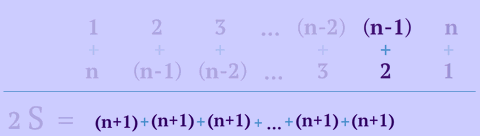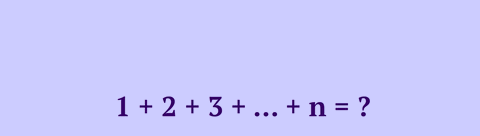Algebraic expressions are mathematical expressions that consists of numbers, variables and mathematical operators.

Terms, factors and coefficients

• Term: A term can be a number, a variable, or a constant multiplied by a variable or variables. Each term in an algebraic expression is separated by a positive sign or negative sign.

• Factors: If algebraic expressions are expressed as the product of numbers, variables or expressions, then each of these numbers and expressions is called the factor of algebraic expressions.

• Coefficients: When a term of an algebraic expression is made up of a constant multiplied by a variable or variables, then that constant is called a coefficient of the algebraic expression.

Monomials, Binomials, & Polynomials

Like & Unlike terms

Addition & Subtraction of Algebraic Expressions

• Horizontal method of addition:
  Step1: Suppose we have to add 3 expression 1a+2b+3c, 4a+5b+6c, and 7a+8b+9c
  Step2: write the expression in a horizontal line and then add all the like terms:

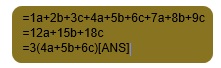
• Column Method of addition:
  Write the 3 expressions in 3 rows with like terms below each other and then add the like terms column-wise.

• Subtraction of algebraic expression:
  Step1: Suppose we have to subtract 10a+23b+45c from 67a+89b+20c

Step2: Write the above expressions in two rows such that the like terms occur one below the other. Keep the expression to be subtracted in the second row.

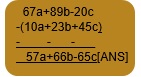
Multiplication of algebraic expressions

• In multiplication of algebraic expressions:
  (i) The product of two factors having like signs is positive, and the product of two factors having unlike signs is negative.
  (ii) if a is a variable and p, q are positive integers, then

• Multiplication of Two Monomials:
  Product of two monomials = (product of their numerical coefficients) × (product of their variable parts)

Example 1: 1ab and -2a²b³

SOLUTION: (1ab) × (-2a²b³)

= {1 × (-2)} × {ab × a²b³}

= -2 x a¹⁺² x b¹⁺³

= -2a³b⁴.

• Multiplying a polynomial by a monomial:

Multiply each term of the polynomial by the monomial, using the distributive property p × (q + r) = p × q + p × r.

EXAMPLE 2: 1x²y² × (2x² - 3xy + 4y²)

SOLUTION: 1x²y² × (2x² - 3xy + 4y²)

= (1x²y²) × (2x²) + (1x²y²) × (-3xy) + (1x²y²) × (4y²)

= 2x⁴y² - 3x³y³ + 4x²y⁴

• Multiplying a polynomial by a polynomial:
  
  Suppose (x + y) and (p + q) are two polynomials. By using the distributive property of multiplication over addition twice, we may find their product as given below.
  
  EXAMPLE 3: Multiply (1a³ – 2a² – a + 3) by (4 – 5a + 6a²)

SOLUTION: Arranging the terms of the given polynomials in descending power of a and then multiplying:

1a³ – 2a² – a + 3

× (4 – 5a + 6a²)
_________________________________
6a⁵ - 12a⁴ – 6a³ + 18a² ⇐ multiplication by 6a².

- 5a⁴ + 10a³ + 5a² – 15a ⇐ multiplication by -5a.

+ 4a³ – 8a² - 4a + 12 ⇐ multiplication by 4.
_________________________________
6a⁵ – 17a⁴ + 8a³ + 15a² – 19a + 12 ⇐ multiplication by (4 – 5a + 6a²)
_________________________________

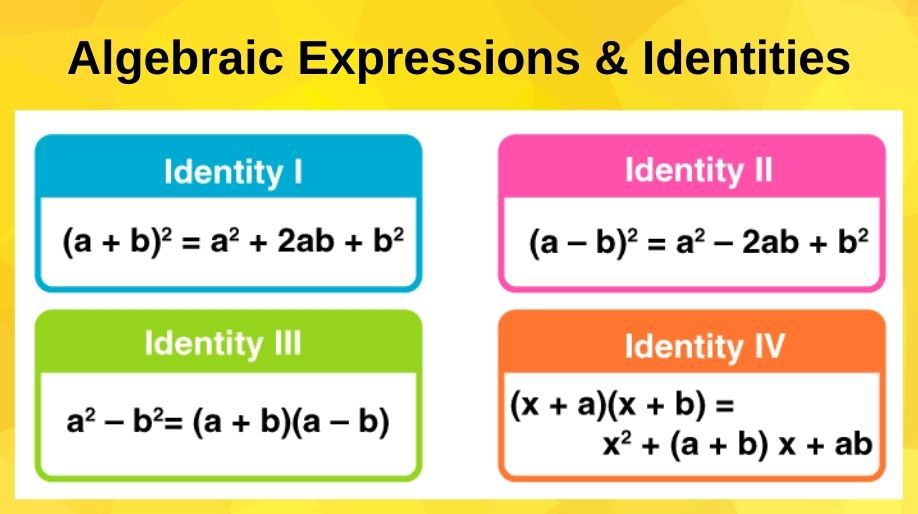
Identities and its applications

• If an equation is true for all values of the variables in it, then that equation is called an identity.

• Some standard identities are:
  
  

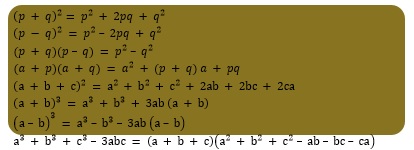
EXAMPLE 1: Expand (a – 2b)³ using standard algebraic identities.

SOLUTION: (a– 2b)³ is of the form (a-b)³ where a = a and b = 2b. So we have,

(a – 2b)³ = (a)³ – (2b)³– 3(a)(2b)(a – 2b) = a³ – 8b³ – 6a²b + 12ab² [ANS]

EXAMPLE 2: Find . Given = 12 and ab=3.

SOLUTION:

Practice these questions

Q1) Multiply the following:
a) 11x²y and 3 b)12 and 33 c)4 and 6

Q2) Find the value of when

Q3) Simplify the following:
a) (x+2y)(3x+4y) – (5x+6y)(7x+8y) b)(9a+10b)(2x+3y) – (4a+5b)(6c+7d)

Q4) Find the product of the following using identities:
a)(8x+9y)(8x-9y) b)(10x+11y+23z)² c)(45a-6b)³ d)(7a+8b)³

Q5) Simplify using identities:
a)121 x 121 – 1001² b)999² c)101² d)

Q6) If , find the value of .

Q7) Find the value of x if 12x=

Q8) Tick the pair of like terms:

Q9) If , find the value of .

Recap

• Algebraic expressions are mathematical expressions that consists of numbers, variables and mathematical operators.
• A term can be a number, a variable, or a constant multiplied by a variable or variables. Each term in an algebraic expression is separated by a positive sign or negative sign.
• If algebraic expressions are expressed as the product of numbers, variables or expressions, then each of these numbers and expressions is called the factor of algebraic expressions.
• When a term of an algebraic expression is made up of a constant multiplied by a variable or variables, then that constant is called a coefficient of the algebraic expression.
• Algebraic expressions which contain one non-zero term only are called monomials.

Algebraic expressions which contain two non-zero terms are called binomials.