• Mensuration is the branch of geometry that deals with the measurement of length, area, and volume.

Area of Trapezium

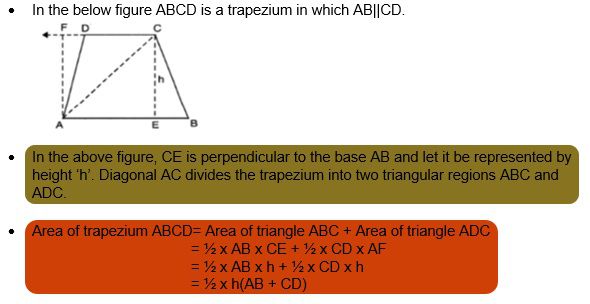
EXAMPLE 1: The parallel sides of a trapezium are AD= 12cm and BC= 30cm and its non-parallel sides are CD= 56cm and AB= 78cm. Find the area of the trapezium.

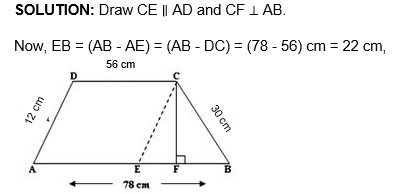
Therefore, 112 + 2x = 123

⇒ 2x = (123 - 112)

⇒ 2x = 11

⇒ x = (11/2)

⇒ x = 6.5

Hence, the length of the other side is 6.5 cm.

Area of a general quadrilateral

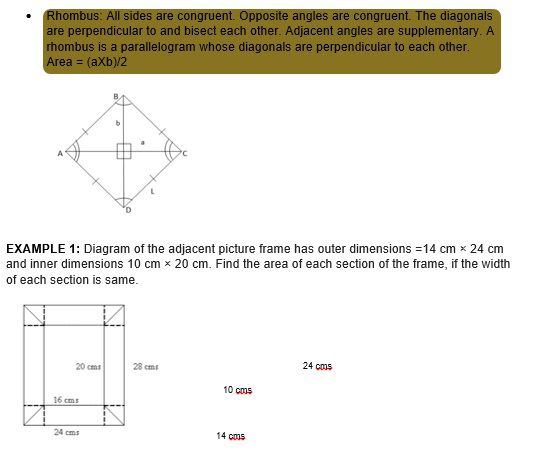
SOLUTIONS: Let us draw a perpendicular from any side of the inner rectangle to the side of

the outer rectangle as shown above. This will give us 4 congruent triangles as 14-10 =

4 and 24-20 = 4 and width of each section is same

So Height and Base of each triangle are 2 cm each

Sides of Both Horizontal Rectangles= 2 cm and 10 cm

Sides of Both vertical Rectangles= 2 cm and 20 cm

Now area of each Triangle= (1/2) ×2×2= 2 cm^2

Area of the horizontal rectangle = 2 x 10 = 20

Hence, Area of lower horizontal section of the frame = 20 + 2 + 2 = 24 cm^2

Area of the vertical rectangle = 2 x 20 = 40

Hence, Area of One Vertical Section of the frame = 40 + 2 + 2 = 44 cm^2

EXAMPLE 2: There is a pentagonal shaped park as shown in the figure. For finding its area Arnav and Meera divided it in two different ways. Find the area of this park using both ways. Can you suggest some other way of finding its area?

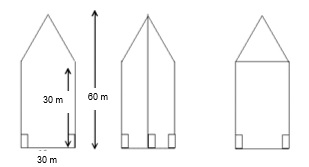
SOLUTION:

Arnav has divided the park into two congruent trapeziums. The parallel sides of the trapezium are measuring 30 m and 60 m and the perpendicular distance is 15 m
Area of each Trapezium=
= (1/2) × (Sum of parallel sides) × Perpendicular distance
= (1/2)(30+60) 15= 675 m²
Area of total park= 2 x Area of each Trapezium = 2 x 675 m^2 = 1350 m^2
Meera divided the park into upper triangular portion and lower rectangular portion. Sides of the rectangle are 30 m each. Base and height of the triangle are 30 m each.
Area of square= 30×30=900 m²
Area of Triangle= (1/2) ×30×30= 450
Total Area = 900 + 450 = 1350 m²

Area of a Polygon

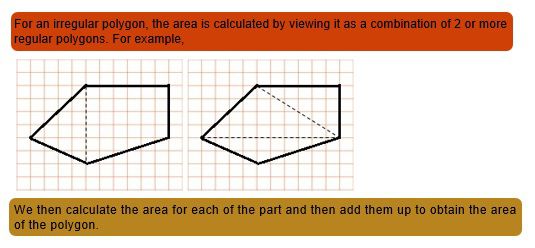
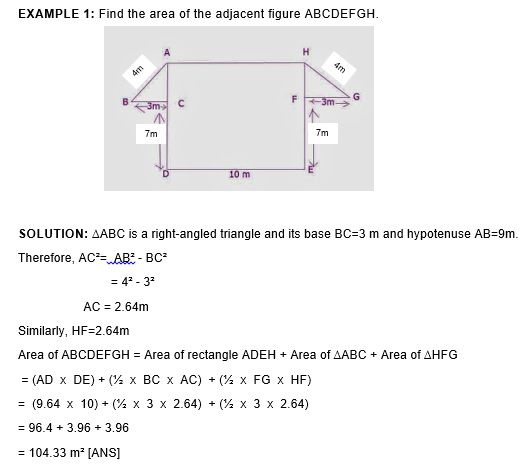
EXAMPLE 2: Find the area of the adjacent regular hexagon PQRST in which each side measures 12m and its height is 34m.

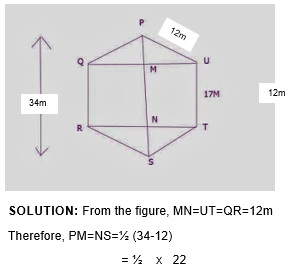
= 11m

Solid Shapes

• Solid shapes are three-dimensional objects which have a width, a depth, and a height.

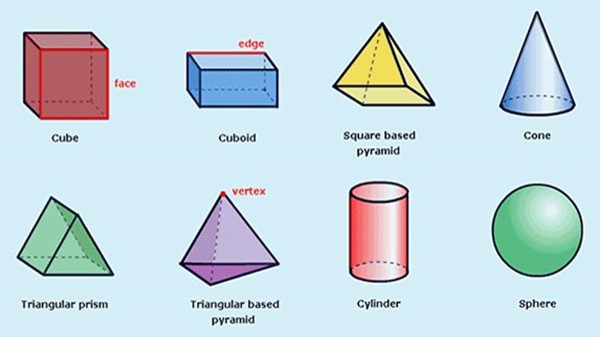
Surface area of cube, cuboid, and a cylinder

• rectangle is the height of the cylinder, h. The length, l, of the rectangle is equal to the circumference of the circle, 2