We all have been studying the term polynomials from lower classes; we know what variables, expressions are and how to solve basic equations. Here we will extend our discussion to some of the theorems used in the polynomials with a beginning from basics.
- In mathematics, a polynomial is an expression consisting of variables and coefficients that involves only the operations of addition, subtraction, multiplications.
- A variable is denoted by a symbol that can take any real value. We use the letters x, y, z, etc. to denote variables.
- The values of the constants remain the same throughout a particular expression, that is, the values of the constants do not change in a given problem, but the value of a variable can keep changing.
Polynomials in One Variable
The polynomial expression in which we have only one variable in the whole expression is called as a polynomial in one variable. For example: x2+4, 2x-1, x3+3x2-7x+4, etc. are all polynomials in one variable x.
- Each individual value in an expression is called as a term of the expression. For example in x2+3x, x2 and 3x are the terms.
- The constant present with each of the individual term is called as a coefficient of that term. For example in the above expression, the coefficient of 3x is 3 and that of x2 is 1.
- The constants 4, 5, -8, -3, etc. are called as constant polynomials and 0 is called as zero polynomial.
- The polynomial having only two terms is called a binomial and with three terms is called a trinomial.
- The highest power of the variable is called as the degree of the polynomial.
- The degree of a non-zero constant polynomial is zero.
- A polynomial with degree two is called a quadratic polynomial and with degree 3 is called a cubic polynomial.
- The general form of a polynomial is
anxn + an-1xn-1 + an-2xn-2…… a0, where an, an-1.........a1,a0 are all constants.
Zeros of a Polynomial
Let us assume that p(x) is a polynomial of degree n, and then the value of x for which the value of p(x) becomes zero is called as the zero of a polynomial.
- A non-zero constant polynomial has no zero.
- Every real number is a zero of the zero polynomial.
Example 2: Verify 5 and 0 are the zeros of the polynomial x2-5x.
Solution: Let p(x) = x2-5x
And p(5) = 25 – 25 = 0
And p(0) = 0-0 = 0
Since p(5) and p(0) are both zero therefore, yes they are the zeros of the polynomial.
Remainder Theorem
When we divide two numbers either they get completely divisible or we get a remainder.
The remainder is a value obtained on division of numbers which cannot be divided further.
We all know that
Dividend = Quotient x Divisor + Remainder
If p(x) and g(x) are any two polynomials with g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that
p(x) = g(x) × q(x) + r(x)
This result is known as Division Algorithm.
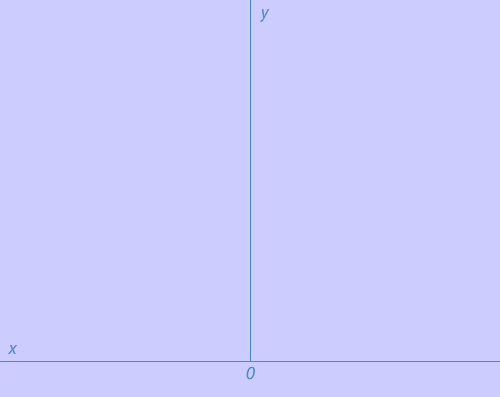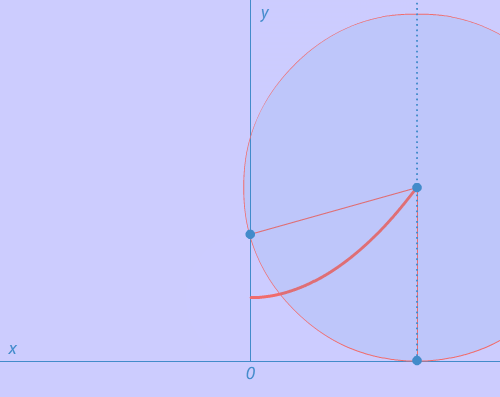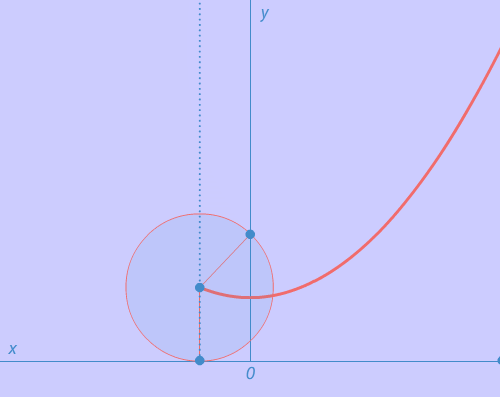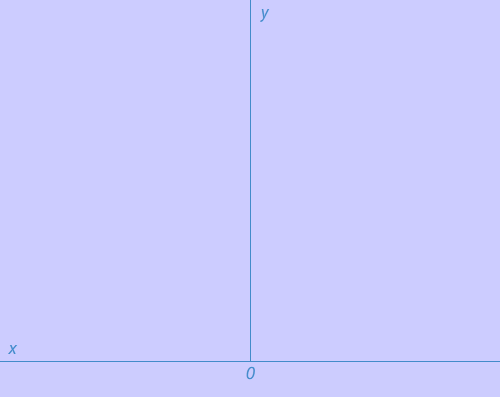
Now let’s see the below example and learn how do we divide two polynomials.
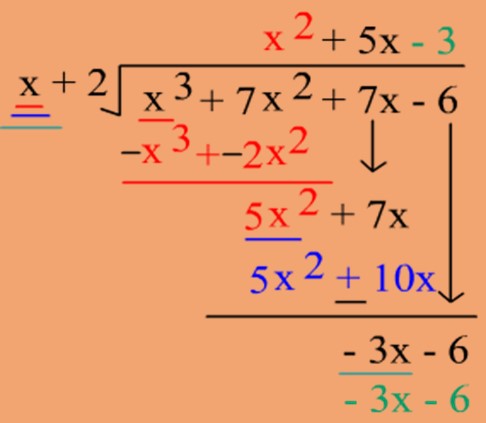
The above figure explains how do we divide two polynomials. Here an important point is to be remembered that the degree of the dividend must be greater than or equal to the degree of a divisor.
In other words, the degree of the divisor must be less than or equal to the degree of the dividend.
Remainder Theorem: Let p(x) be any polynomial of degree greater than or equal to one and let ‘a’ be any real number. If p(x) is divided by the linear polynomial x – a, then the remainder is p(a).
Example 3: Find the remainder when x4+x3-2x2+x+1 is divided by x-1.
Solution: here p(x) = x4+x3-2x2+x+1, and the zero of x-1 is 1.
p(1) = (1)4+(1)3- 2(1)2 + 1+1= 2.
And hence the remainder is 2.
Factorization of Polynomials
- Factorizing polynomials means breaking of the whole expression in simple expressions (majorly linear) so that when these are multiplied they generate the whole expression again.
- A factor will always have a degree less than the polynomial.
Factor Theorem: If p(x) is a polynomial of degree n ≥ 1 and a is any real number, then
(i) x – a is a factor of p(x), if p(a) = 0, and
(ii) p(a) = 0, if x – a is a factor of p(x).
Example 4: Factorize y2 – 3y + 2 by using the Factor Theorem.
Solution: Let p(y) = y2 – 3y + 2. Therefore from factor theorem p(y) = (y-a)(y-b) where a and b are the roots of the equation.
Now ab = 2 hence on factorizing we get 2 and 1.
P(2) = 22- 6 +2 = 0
P(1) = 12 –3 + 2 = 0.
And hence (p-2) and (p-1) both are the factors of the polynomial y2 – 3y + 2.
Algebraic Identities
In the field of mathematics there are certain algebraic identities which help us in simplifying the expressions among which few are mentioned below:
- i) (x+y)2 = x2+y2+2xy
- ii) (x-y)2 = x2+y2-2xy
iii) (x2-y2)= (x+y)(x-y)
- iv) (x+a)(x+b)=x2+ (a+b)x+ ab
- v) (x+y+z)2= x2+y2+z2+2xy+2yz+2zx
- vi) (x+y)3= x3+y3+3x2y+3xy2
vii) (x-y)3= x3-y3-3x2y+3xy2
viii) x3+y3+z3-3xyz = (x+y+z)(x2+y2+z2-xy-yz-zx)
Example 5: Evaluate the value of (103)3.
Solution: (103)3 = (100 + 3)3 and hence by using the identity 6 we get,
(103)3 = (100 + 3)3 = (100)3 + 33+ 3x3x (100)2 + 3x100x(3)2
(103)3 = 1000000 + 27 + 90000 + 2700 = 1092727.
Practice Questions
Q1) Evaluate the value of (209)3.
Q2) If x+y+z=0, then show that x3+y3+z3= 3xyz.
Q3) Factorize x3-2x2-x+2.
Q4) Check whether (x+2) is a factor of x3-2x+ 4 or not.
Q5) Find the value of the polynomial 5x3- 3x2+4x+1 at
- i) x=1 ii) x=3 iii) x=4 iv) x=0
Recap
- A polynomial of one term is called a monomial and a polynomial of two terms is called a binomial and a polynomial of three terms is called a trinomial.
- A polynomial of degree one is called a linear polynomial and a polynomial of degree two is called a quadratic polynomial.
- A real number ‘k’ is a zero of a polynomial p(x) if p(k) = 0. In this case, k is also called a root of the equation p(x) = 0.
- Every linear polynomial in one variable has a unique zero, a non-zero constant polynomial has no zero, and every real number is a zero of the zero polynomial.
- Remainder Theorem: If p(x) is any polynomial of degree greater than or equal to 1 and p(x) is divided by the linear polynomial x – a, then the remainder is p(a).
- Factor Theorem: (x – a) is a factor of the polynomial p(x), if p(a) = 0. Also, if (x – a) is a factor of p(x), then p(a) = 0.
- The general form of a polynomial is
anxn + an-1xn-1 + an-2xn-2…… a0, where an, an-1.........a1,a0 are all constants.
- If p(x) and g(x) are any two polynomials with g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that
p(x) = g(x) × q(x) + r(x)
This result is known as Division Algorithm