Lines and Angles

We all know that to draw a line we require minimum two points. When two lines are drawn, they can either be parallel or they can be intersecting each other. Here we are going to learn about the angles which lines make when they intersect and the properties of the angles.

Let us start from some basic terminologies and revise them:

Line: A line is a straight path extended to both the direction such that it doesn’t have any endpoints.

Line Segment: A line segment is a part of a line having two endpoints.

Ray: A ray is a part of a line having a single endpoint only.

If three points lie on the same line, they are called as collinear points or else they are called as non-collinear points.

Acute Angle: When the measure of an angle is less than 90°.

Obtuse Angle: When the measure of the angle is greater than 90°.

Straight Angle: When the measure of an angle is 180°.

Reflex Angle: When the measure of an angle is greater than 180° and less than 360°.

Right Angle: When the measure of the angle is exactly 90°.

• If the sum of two angles is 90°, they are said to be complementary angles and if the sum is 180°, they are said to be supplementary angles.
• Two angles are adjacent so they share a common vertex.

Intersecting and Non-intersecting Lines

When two lines are parallel to each other, they can never meet at any point and hence they are said to be non-intersecting lines.

When two lines are not parallel, it is definite that they are going to meet at least at a single point and hence they are said to be intersecting lines.

Pairs of Angles

Here we are going to learn about the angles and the properties of these angles.

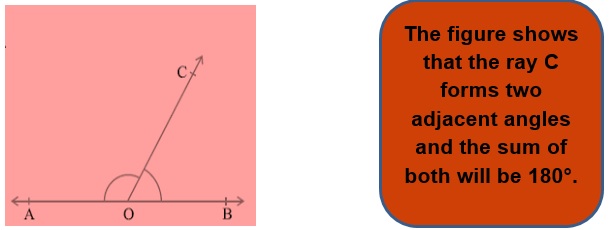
• If a ray stands on a line, then the sum of two adjacent angles so formed is 180°.

• If the sum of two adjacent angles is 180°, then the non-common arms of the angles form a line.

The above two are actually axioms and together are known as linear pair axioms.

Parallel Lines and Traversal

A line which intersects two or more lines at distinct points is called as a traversal.

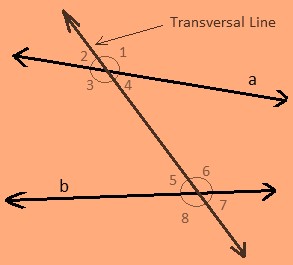
The above figure shows the traversal line which intersects the two lines a and b at two distinct points.

Here we can draw some conclusions from the above figures which are:

1) Angles 1, 2, 7 and 8 are exterior angles.

2) Angles 3, 4, 5 and 6 are interior angles.

Corresponding Angles:

1. a) 1 and 5 b) 2 and 6
2. c) 3 and7 c) 4 and 8

Alternate Interior Angles:

1. a) 4 and 6 b) 3 and 5

Alternate exterior Angle:

1. a) 1 and 7 b) 2 and 8

• Interior angles on the same side of the transversal are also referred to as consecutive interior angles or allied angles or co-interior

• Here the consecutive interior angles are a) 4 and 5 and b) 3 and 6.

There are certain axioms related to the traversal lines, let’s learn about them:

• If a transversal intersects two parallel lines, then each pair of corresponding angles is equal.

• If a transversal intersects two lines such that a pair of corresponding angles is equal, then the two lines are parallel to each other.

Angle Sum Property of Triangle

According to the angle sum property of a triangle, the sum of all the interior angles of any triangle will be 180°.

Theorems

Here we are going to discuss about the various theorems which are related to the topic and hence we will learn how to use these while solving the questions.

• Theorem 1: If two lines intersect each other, then the vertically opposite angles thus formed are equal in measure and vice versa.

• Theorem 2: If a traversal intersects two parallel lines, then each pair of alternate angle will be equal in measure.

• Theorem 3: If a traversal intersects two parallel lines, then each pair of interior angles on the same side of the traversal is supplementary and vice versa.

• Theorem 4: Lines parallel to the same line are parallel to each other. In simple words, it means, if a line A is parallel to the line B, and a line C is parallel to the line B also. Then the two lines A and C will also be parallel to each other.
• Theorem 5: If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.

Example 1: Find the value of a, b and c.

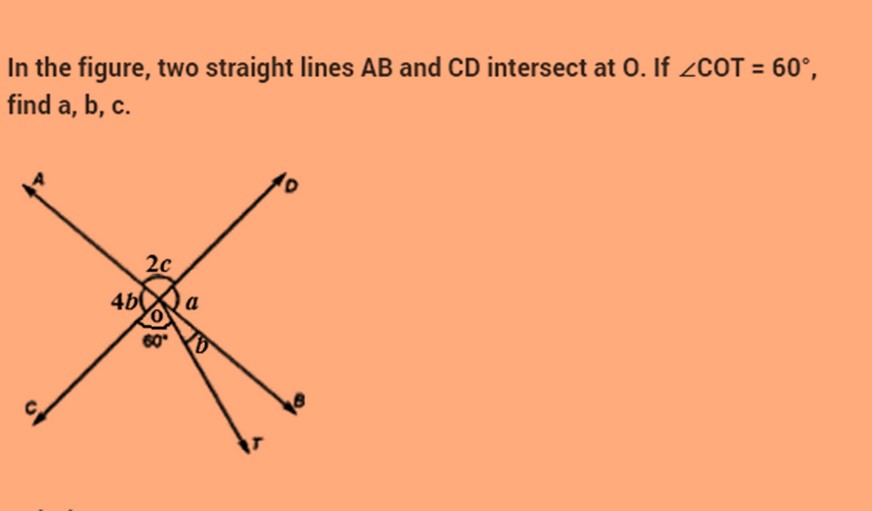
Solution: Since AB and CD intersect at O

It means that angle BOD = angle AOC

It means a = 4b

And a + b + 60° = 180°

And a + b = 120°which means

4b + b = 120° and hence we get the value of b=24°.

And hence a = 96°.

As we know that sum of adjacent linear angles is 180° and hence,

a + 2c = 180°.

And on putting the value of a, we get

2c = 180°-96° = 84°

And hence c = 42°.  

Example 2: Find the value of x

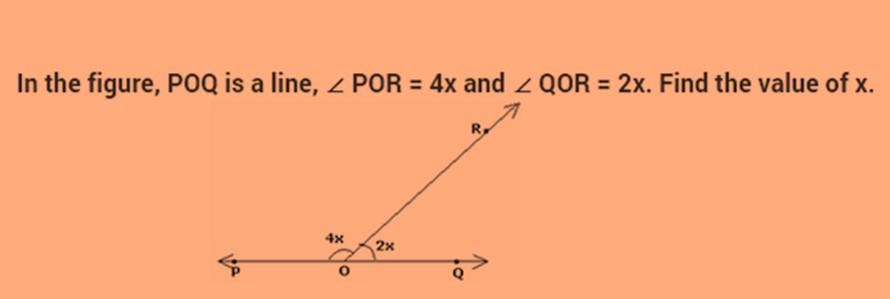
Solution: As we know that the sum of the adjacent linear angles formed by the ray is 180°.

Therefore 4x+2x=180°.

6x=180°

And hence we get the value of x as 30°.

Example 3: In the given figure if the measure of the angle NOY is 60°, then Find the value of angles a, b and c.

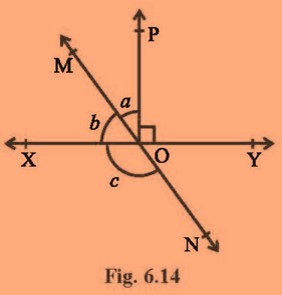
Solution: As we can see that angle NOY and b are vertically opposite angles, hence

Angle b = angle NOY = 60°.

Now as we know that the sum of the adjacent linear angles formed by the ray is 180°.

Therefore: a + b + 90° = 180°.

a + b = 90°.

a + 60° = 90° and hence the value of ‘a’ comes out to be 30°. 

Now from the same property, we can also say that

b + c =180°

and hence the value of c comes out to be 180°- 60° = 120°.

Practice Questions

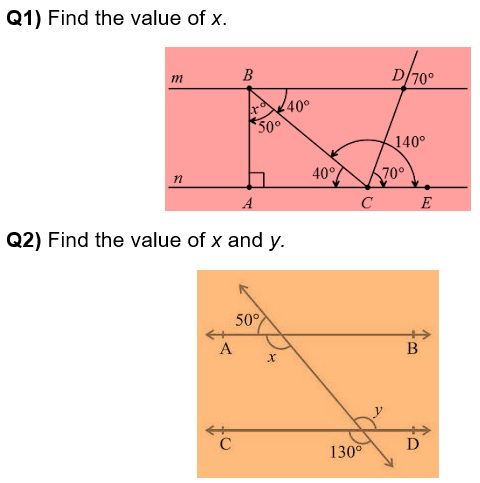
Q3) Fill in the blanks:

1. Alternate interior angles are on the________ side of the triangle.
2. The supplement of a right angle is always ________angle.
3. Two angles forming a ____ pair are supplementary.
4. If the sum of measure of two angles is 90°, then the angles are _________.

Recap

• If a ray stands on a line, then the sum of the two adjacent angles so formed is 180° and vice-versa. This property is called as the linear pair axiom.

• Lines which are parallel to a given line are parallel to each other.

• The sum of the three angles of a triangle is 180°.

• If two lines intersect each other, then the vertically opposite angles are equal.