Quantity is the extent, size or sum of countable or measurable discrete events, objects or phenomena. One can compare quantities if one has knowledge of ratios, discounts, and percentages. Let’s us learn more about them in detail in the upcoming sections.

Ratios and Percentages

• In the ratio, a:b, a is called antecedent and b is called consequent.

• The ratio of two numbers is always expressed in the lowest form.
  
  For example,
  If the ratio of two quantities is 17:34.
  Then, reduce it to 1:2 [17 X 2 = 34]

• The order of the ratio is important. If we interchange the antecedent and the consequent then we get a different ratio.
  
  For example,
  1:2 ≠ 2:1

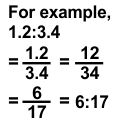
The antecedent and consequent in a ratio are always whole numbers. When they are not, convert them into whole numbers.

• Multiple percentages are not additive in nature.

EXAMPLE 1: Two numbers are in the ratio 1:23. On adding 4 to the first and 5 to the second, their ratios become 1:13. Find the numbers.

SOLUTION: Let the numbers be 1x and 23x.

Adding 4 to the first number, we get= 1x + 4

Adding 5 to the second number, we get= 23x + 5

The ratio of new numbers are in the ratio (1x + 4) : (23x + 5) which is equal to 1:13

Thus, (1x + 4) : (23x + 5) = 1:13

(1x + 4)/(23x + 5) = 1/13

13(1x + 4) = 1(23x + 5)             [Doing cross multiplication]

13x + 52 = 23x + 5

10x = 47

x = 4.7

Hence, the numbers are 4.7 and 23X4.7= 108.1 [ANS]

EXAMPLE 2: Out of the salary of Rs.123456, I kept 1/2 as savings. Out of the remaining money, I spend 47% on food and 18% on rent. How much do I spend on food and house rent?

SOLUTION: My salary is Rs. 123456

My savings s = 1/2  x  123456 = Rs. 0.61728

Remaining Money= Rs. (123456 - 61728) = Rs. 61728

Amount of money I spend on food = 47% x 61728 = (47/100) x 61728 = 0.47 x 61728

                                                                                                       = Rs. 29012.16

Amount of money I spend on rent = 18% x 61728 = 18/100 x 61728 = 0.18 x 61728

                                                                                                     = Rs. 11111.04

Hence, I spend Rs.29012.16 on food and Rs.11111.04 on rent. 

Increase or Decrease Percent

To find the increase in percentage, work out the increase between the two numbers to be compared. Then, divide the increase by the original number and multiply the quotient by 100.

 To find the decrease percent, work out the difference between the two numbers you are comparing. Then divide the decrease by the original number and multiply the quotient by 100.

EXAMPLE 1: The population of a town in a particular year increased by 10%. Next year it decreased by 10%. Find the net increase or decrease percent in the initial population.

SOLUTION: Let the initial population of the town be x.
Population increased by= 10% X x= 0.1 X x =0.1x
Increase Population= (x+0.1x)= 1.1x
Next year, population decreased by= 10% X 1.1x= 0.1 X 1.1x= 0.11x
Decreased population= 1.1x- 0.11x= 0.99x
0.99x<x, clearly the population decreased.

Decrease percent = x - 0.99x/x x 100 = 1%

Hence, the decrease in population is 1%. 

EXAMPLE 2: The price of onions increased by 12%. By how much percent should you reduce your consumption in the house so that your expenditure on onions does not increase?

SOLUTION: Decrease in consumption= {[%Price Increase]/[100 + % Price Increase]} X 100

                                                     = 12/[100 + 12] x 100

                                                     = (12/112) x 100 = 10.7%

 Hence, I should reduce my consumption by 10.7% if the price of onions has increased by 12%.

Hence, I should reduce my consumption by 10.7% if the price of onions has increased by 12%.

Finding Discounts

Convert the percentage discount to a decimal.

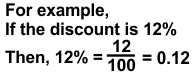
• Subtract the discount from the original price
  
  For example,
  Discounted price for the shoes = Rs.(3456 - 414.72)
                                               = Rs. 3041.28

EXAMPLE 1: An item marked at Rs.1234 is sold for Rs.567. What is the discount and discount%?

SOLUTION: Discount Amount= Rs.(1234 – 567)= Rs. 667
Percentage Discount = (Discount Amount)/(Marked Price) X 100
                              = 667/1234 X 100
                              = 54.05%

Hence, Discount= Rs.667; Percentage Discount= 54.05% 

EXAMPLE 2: The list price of a dress is Rs.8901. A discount of 23% is announced on sales. What are the amount of discount on it and its sales price?

SOLUTION: Amount of discount= 23% X Rs.8901= Rs.2047.23
Sales Price= Rs.[8901- 2047.23] =Rs.6853.77

Hence, discount amount= Rs2047.23; sales price=Rs.6853.77. [Ans]

Profit & Loss

Cost Price: The price at which an article is purchased is called its cost price. It is abbreviated as CP. 

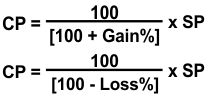
Selling Price: The price at which an article is sold is called its selling price. It is abbreviated as SP.

If the selling price is more than the cost price, the seller is said to have a profit or gain.

If the selling price is less than the cost price, the seller is said to have incurred a loss.

EXAMPLE 1: Arya sold two digital cameras at Rs. 30,000 each. On one she gains 12% and on the other, she loses 12%. What percent does she gain/loss on the transaction?

SOLUTION: For the first digital camera:

 Gain= 12%

Let cost price(CP) = Rs. 100

Therefore, Selling Price(SP) = Rs. [100 + 12%/100] X 100= Rs.112

When the selling price is Rs.112, Cost Price is Rs. 100.

When the selling price is Re. 1, Cost Price = Rs. 100/112

When the selling price is Rs.30, 000, Cost Price = Rs. (100/112) x 30000 = Rs. 26785.71

For the second digital camera:

Loss = 12%

Let cost price is Rs. 100.

Therefore, Selling Price-Rs. (100 - 12) = Rs. 88

When the selling price is Rs.88, cost price is Rs. 100.

When the selling price is Re. 1, cost price is Rs. 100/88.

When the selling price is Rs.30000, Cost Price is Rs. (100/88) X 30000 = Rs.34090.90

The total cost price of two digital cameras = Rs (26785.71+34090.90) = Rs.60876.61

The total selling price of two digital cameras = Rs. 2 X 30000= Rs.60,000

Thus, cost price > selling price, so there is a loss.

Loss CP - SP = Rs. (60876.61 - 60000) Rs. 876.61 

Loss Percentage= Loss/CP X 100 = 876.61/60876.61 X 100 = 1.4% 

Hence, Arya loses 1.4% on the whole transaction.

Alternative Method:
If two commodities are sold at the same price and the seller gets the same amount of gain & loss on each commodity then the seller always incurs a loss on the whole transaction.

Loss% = [Common Loss or Gain%/10]² = [12/10]² = 1.44%. 

EXAMPLE 2: Krishna bought a laptop for Rs. 123456 and spent Rs.7890 on its spares. He later sold the laptop for Rs. 234567. Find her gain or loss percent.

 SOLUTION: Cost price includes the overhead expenses also.

Therefore, cost price = Rs. (123456 + 7890) = Rs. 131346

And SP = Rs. 234567

Since Selling Price > Cost Price, there is a profit.

Profit = SP - CP = Rs. [234567 - 131346] = Rs.103221

Profit% = Profit/CP X 100 = 103221/131346 x 100 = 78.5%

Hence, her total profit is 78.5%. 

Sales Tax / Value-Added Tax

Sales Tax is calculated on the sales price.

• Value Added Tax (VAT) is a tax on the value added at each transfer of goods, from the original manufacturer to the retailer.
  
  For example,
  Assuming the rate of tax is 12% and a person purchases an article for Rs.345.
  The tax he pays= Rs.(12% X 345) = Rs. 41.4
  Now, if he sells the same article for Rs. 678
  The tax he recovers= Rs.(12% X 678) = Rs. 81.36
  VAT = Tax recovered on the sale – Tax he paid on the purchase
         = Rs.(81.36 – 41.4) = Rs.39.96

EXAMPLE 1: Swathi bought the following articles from a departmental store

Calculate the total bill paid, including sales tax paid by Swathi to the departmental store.

SOLUTION: Cost price of 3 dress= Rs.1234 X 3 = Rs.3702
Sales tax on dresses = Rs. (12% X 3702) = Rs. 444.24
Amount paid for 3 dresses = Rs(3702+444.24) = Rs 4146.24

Cost price of 2 bags= Rs 567 X 2 = Rs 1134
Sales Tax on 2 bags = Rs (3% X 1134) = Rs 34.02
Amount paid for 2 bags = Rs(34.02+1134) = Rs1168.02

Cost Price of 1 Laptop = Rs89012
Sales Tax on Laptop = Rs. (4% X 89012) = Rs.3560.48
Amount paid for 1 laptop = Rs. (89012 + 3560.48) = Rs.92572.48

Cost Price of 2 dinner set = Rs. (2 X 345) = Rs. 690
Sales Tax on 2 dinner sets= Rs(5% X 690) = Rs.34.5
Amount paid for 2 dinner sets = Rs.(34.5+690) = 724.5

Hence, total amount of bill = Rs.[4146.24+1168.02+92572.48+724.5) = Rs.98611.24

EXAMPLE 2: A shopkeeper bought an AC at a discount of 12% from the wholesaler, the printed of the AC is Rs.34567. The shopkeeper sells it to a consumer at a discount of 8% on the printed price. If the rate of sales tax is 9%, find i) the VAT paid by the shopkeeper.
ii) the total amount that the consumer pays for the AC.

SOLUTION: M.P. = Rs.34567
Discount= 12% for shop-owner
Discount = 8% for consumer
Sales Tax = 9%

Discount for shopkeeper = Rs.(12% X 34567) = Rs. 4148.04
Cost for Shopkeeper = Rs(34567 – 4148.04) = Rs. 30418.96

Cost for Consumer = Rs(34567 – (8% X 34567)) = Rs. 31801.64

31801. Tax charged by the shopkeeper= Rs.(9% X 31801.64) = Rs. 2862.1476
       Tax paid by the shopkeeper = Rs.(9% X 30418.96) = Rs.2737.7064
       Hence, VAT paid by the shopkeeper = Rs.(2862.1476 – 2737.7064) = Rs. 124.44

31801. Amount paid by the consumer = Rs.(31801.64 +2862.1476) = Rs. 34663.78[Ans]

Compound Interest

• Compound Interest is the interest calculated on the principal amount and also on the accumulated interest of previous periods.

• When interest is compounded annually:

  

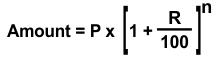
• When interest is compounded half-yearly:

  

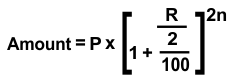
• When interest is compounded quarterly:

  

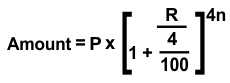
• When interest is compounded annually but the time is in fraction, say 1 2/3 years

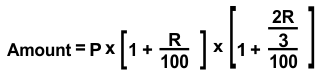
• When rates are different for different years say R1%, R2%, and R3% for three consecutive years, then:

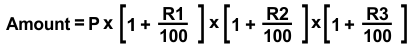
EXAMPLE 1: Calculate the amount and compound interest on Rs.12, 345 for 6 7/8 years at 9% per annum compounded annually.

SOLUTION:

Amount = Rs. 12345 X [1 + 9/100]⁶ x [1 + {(7 x 9/8)/100}] = Rs. 22334.22 

Compound Interest = Amount - P = Rs.(22334.22 - 12345) = Rs. 9989.22 

EXAMPLE 2: Sonal borrowed Rs.23456 from a Bank to buy a bike at a rate of 7% p.a. compounded yearly. What amount will she pay at the end of 8 years and 9 months to clear the loan?

SOLUTION: 9 months = 9/12 years = 3/4 years

Total years = 8 ¾  years

Amount = Rs.23456 x [1 + 7/100]⁸ × [1 +3 x 7/4/100] = 42,417.61 

Practice these questions

Q1) The ratio of the number of boys and a number of girls in a school of 1234 students is 5:6. If 78 new boys are admitted, find how many new girls should be admitted to make the ratio 1:2.

Q2) Rachel gets 91 marks in her exam. These are 23% of the total marks. Find the Maximum number of marks.

Q3) Increase 123 by 4% and then decrease it by 5%. Find the final number.

Q4) The marked price of a water cooler is Rs. 14650. The shopkeeper offers an off-season discount of 8% on it. Find its selling price.

Q5) Monica bought 2 dozen eggs for Rs. 156. Since 7 of them broke, he incurred a loss of Rs.120 on selling them. What was the selling price of one egg?

Q6) A manufacturer printed the price of his goods as Rs.1120 per article. He allowed a discount of 4% to the wholesaler who in his turn allowed a discount of 3% on the printed price to the retailer. If the prescribed rate of sales tax on the goods is 5% and the retailer sells it to the consumer at the printed price then find the value-added tax paid by the wholesaler and the retailer.

Q7) Vivan took a loan of Rs. 654987 from the bank. If the company charges interest at 15% per annum, compounded quarterly, what amount will discharge his debt after one year?

Recap

• The percentage is not cumulative in nature.
• Sales taxis are collected by the retailer when the final sale in the supply chain is reached via a sale to the end consumer.
• Compound Interest is the interest calculated on the initial principal and also on the accumulated interest of previous periods of a deposit or loan.