Surface Area and Volumes

We all know about the solids and various kinds and combinations of solids which can be formed. Now in our earlier classes, we have learnt about finding the areas of all the 2D bodies like the square, rectangle, circles. But here we are going to extend our vision to determine the areas of the solid bodies or in simple words 3D bodies.

• Solids are the 3D objects are called as solids. It means that any object which has length, breadth and width is termed as a solid.
• The surface area of a solid object is a measure of the total area that the surface of the object occupies.
• The concept of surface area if taken to the molecular level leads us to the concept of integration of very small 2D areas which finally constitutes the whole area of the solid body.
• And the most common example of this is the surface area of a sphere which is an overall integration of the small circle elements together leading to the area of the circle.
• Volume is the quantity of three-dimensional space enclosed by a closed surface or a solid, for example, the space that a substance or shape occupies or contains.
• In simple words the amount of liquid up to the saturation point of the solid object.

Formulae for the Surface area and Volume of Solids

Combination of solids

When two same or different kinds of solids combine they form a completely new solid whose surface area depends accordingly on the constituent solids.

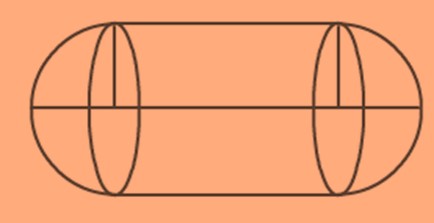
For example, the given solid is a combination of two hemispheres and a cylinder, and hence the total surface area of the solids will depend on the surface areas of the constituent solids which means

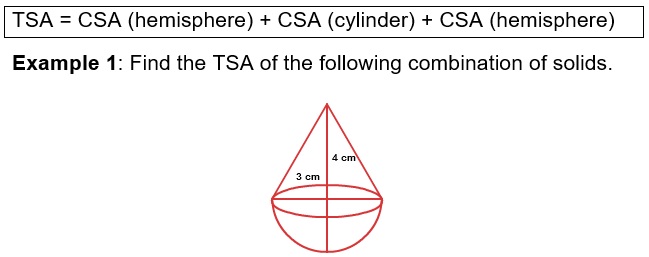
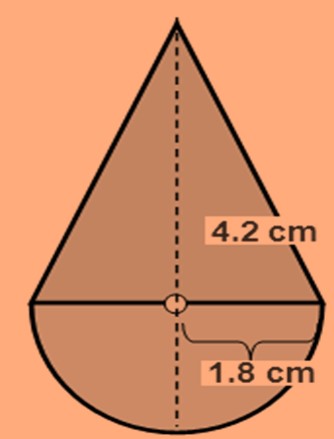
Solution: The solid is the combination of cone and a hemisphere

TSA = CSA of hemisphere + CSA of cone

TSA = 2πr² + πrl

TSA = 2 x 3.14 x 9 + 3.14 x 3 x 4

TSA = 56.52 cm² + 37.68 cm² = 94.2cm²

Example 2: Find the volume of the following combination of solids.

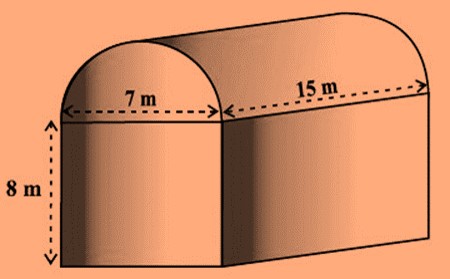
Solution: The above combination is of a cuboid and a half cylinder and hence the total volume of the solid will be:

Total Volume = Volume of cuboid + Volume of half cylinder

Total Volume = lbh + ½ πr²h

= [15 x 7 x 8 m³ + ½ x 3.14 x 3.5 x 3.5 x 15 m³ ]

= 840m³ + 288.45m³ = 1128.45m³

Change of shape of solid

A solid can be changed to different shapes and sizes by melting it and then casting it to any other form. This process is known as casting of solids.

Here an important point is to be remembered that by doing the above process the volume of the solid before and after melting will always remain the same.

Example 3: A metallic sphere of diameter 8.4 cm is melted and recast into a shape of cylinder of diameter 12 cm. Find the height of the cylinder.

Solution: As we know that the volume will be constant

Therefore Volume of sphere = Volume of sphere

4/3πr³ = πr²h

4/3 x 3.14 x 4.2 x 4.2 x 4.2 cm³ = 3.14 x 6 x 6 x h cm³

h = 2.744 cm.

Frustum

When a cone is cut in such a manner that the cutting axis is parallel to the axis of the cone, then the solid obtained is called as a frustum.

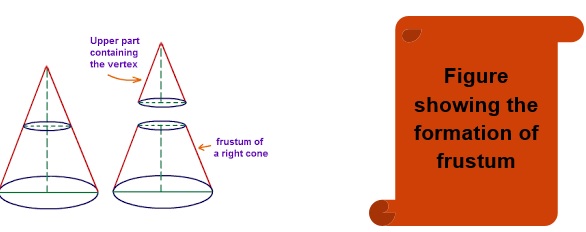
Example 4: Find the TSA and CSA of the frustum of height 14 cm, the radius of the two circular surfaces are 2cm and 4cm.

Solution: TSA = π(r+R)√[(R+r)² + h²] + πr² + πR²

TSA = 3.14 x 6 x √232 cm² + 3.14 x 4 cm² + 3.14 x 16 cm²

TSA = 286.96 cm² + 12.56 cm² + 50.24 cm² = 349.76 cm²

CSA = π(r+R) )√[(R+r)² + h²]

CSA = 286.96 cm².

Areas Related to Circles

A circle is a 2D shape having the radius as one parameter of measurement.

Circumference = 2πr

Area = πr²

We all know about the tangent, secant, major and minor sector as well as segment.

Here we are going to learn about the areas of these parts whioch they occupy in a circle.

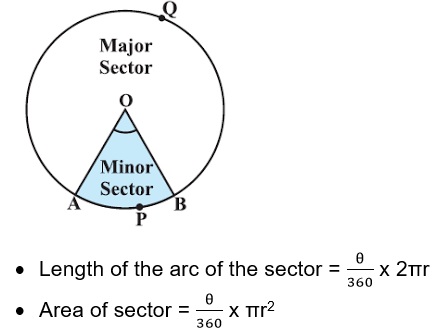
• Area of segment = Area of the corresponding sector – Area of the corresponding triangle.

Example 5: Find the area of the sector and the length of the arc if the substituted angle is 90° and the radius of the circle is 10cm.

Solution: Here we have been given that  = 90° and r = 10cm

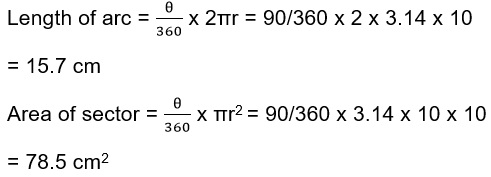
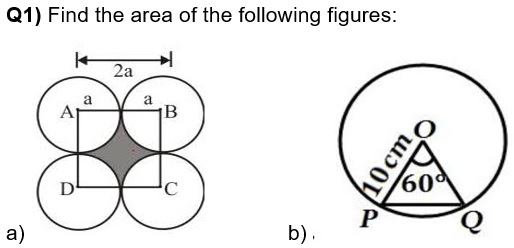
Practice Questions

Q2) Find the area and circumference of the circle having radius 15 cm.

Q3) A drinking glass is in the shape of a frustum of a cone of height 18 cm. The diameters of its two circular ends are 3 cm and 6 cm. Find the capacity of the glass.

Q4) Find the TSA and Volume of the following solid.

Recap

• Given a right circular cone, which is sliced through by a plane parallel to its base, when the smaller conical portion is removed, the resulting solid is called a Frustum of a Right Circular Cone.

• Solids are the 3D objects are called as solids. It means that any object which has length, breadth and width is termed as a solid.

• The concept of surface area if taken to the molecular level leads us to the concept of integration of very small 2D areas which finally constitutes the whole area of the solid body.