- An equation which has only one variable is called Linear Equation
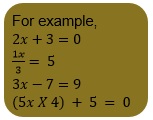
Solving equations which have linear equations on one side and numbers on the other side
EXAMPLE 1: Solve 3x + 15 = 1
SOLUTION:
- We need to keep the variable on the left side and numerical terms on the right side. Because of this, we have to transport 15 to the right side by changing its sign i.e., -15.
=> 3x + 15 = 1
=> 3x = 1-15
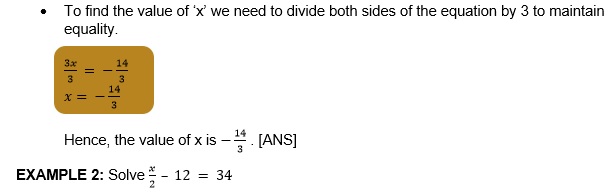
SOLUTION:
- We need to keep the variable on the left side and numerical terms on the right side.
Because of this, we have to transport -12 to the other side by changing its sign i.e., +12.

Solving equations having variables having the variable on both sides
EXAMPLE 1: Solve .
SOLUTION:
- Simplify the given equation.
=>
=>
- Bring the variable terms on the left side of the equation and the other numerical terms on the right side of the equation.
=>
=>
- Now, to find the value of ‘x’ we need to divide both sides of the equation by 6 to maintain equality.

To eliminate the denominator terms, multiply both sides of the equation by the LCM of 6 and 8.

Application of Linear Equations
Linear equations are used to find the value of an unknown quantity. Have a look at the following examples:
EXAMPLE 1: The sum of the digits of a 2 digit number 13. The numbers obtained by interchanging the digits is 14 more than the given number. Find the number.
SOLUTION: Let the digit at units place be x and the number at tens place be y.
=> y + x = 13 [sum is 13 given]
=> y = 13 – x [Transposing x to the other side by changing its sign]
Thus, the formed number is= [Since x is at ones place and y=13-x is
at tens place]
After interchanging the digits, the number is= [Now x is at tens place &
y=13-x is at one's place]
The interchanged number is greater than the original number by 14. [Given]
Therefore,
New number Old number Difference
- Simplify
=>
=>
=>
=>
- Transpose the variable term ‘x’ on the left side of the equation and other numerical terms on the right side of the equation by changing their sign.
=> 18x – 117 = 14
=> 18x = 131
To find the value of ‘x’, divide both sides by 18.
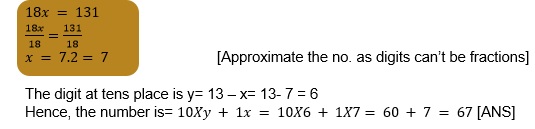
EXAMPLE 2: The distance between town A and town B is 123 km. Two buses begin their journey from these towns and move directly toward each other. From town A, the bus is moving at a speed of 45 km per hour and from town B, the bus is moving at 67 km per hour.
Assuming the buses start at the same time, find how far is their meeting point from town A.
SOLUTION: Let the buses meet after t hours.

We know that distance= speed X time
Distance covered by bus 1 = 45 X t
Distance covered by bus 2 = 67 X t
Therefore, 45t + 67t = 123
The distance travelled by bus 1 from city A to the meeting point= speed of bus 1 X time taken by it to reach the meeting point.
=45 X 1.098= 49.41 km
Thus, the distance of reaching point from town A is 49.41km. [ANS]
Reducing Equation to Simpler Form
Cross Multiplication: We can solve an equation using ratios of linear algebraic equation using the cross multiplication

EXAMPLE 2: The sum of two integers in 81. And the ratio of these integers is 1:2. Find these integers.
SOLUTION: Let one of these integers be x.
The other integer is= 81-x [Since sum of integers is 81; Given]
Given that, x : (81-x) = 1:2
Using cross multiplication we get;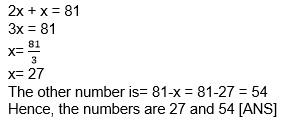
Equations reducible to linear form
Consider the following examples to see how we can reduce equations involving ratios into linear form.

- Now, simplify
=> 6x + 12 + 12x + 15 = 14x + 16
=> 18x + 27 = 14x +16
- Transpose the variable term ‘x’ to the left side and the numerical terms on the right side of the equation by changing their sign.
=> 18x – 14x = 16 – 27
=> 4x = 11
Divide both sides by 4 to find the value of x.
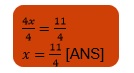
Practice these questions
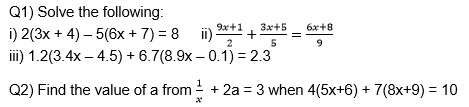
Q3) Three numbers are in the ratio 1:2:3. If the sum of the largest and the smallest equals the second and 45. Find the numbers.
Q4) Find the number whose 1/6th part decreased 7 equals its 8/9th part diminished by 1.
Q5) The difference between two numbers is 23. And the quotient obtained by dividing the larger number by the smaller one is 4. Find the numbers.
Q6) A man cycles to the office from his house at a speed of 5km per hour and reaches 6 minutes late. If he cycles at a speed of 7km/hr, he reaches 8 minutes early. What is the distance between the office and his house?
Q7) Suraj is now half as old as his father. 20 years ago, Suraj’s father was six times Suraj’s age. What are their ages now?
Q8) The perimeter of an isosceles triangle is 91cm. If the length of each equal side is 2cm more than the length of its base. Find the lengths of the sides of the triangle.
Q9) The age of a boy in months is equal to the age of his grandfather in years. If the difference between their ages is 66 years, find their ages.
Recap
- The basic principle used in solving any linear equation is that any operation performed on one side of the equation must also be performed on the other side of the equation.
- Any term in an equation can be transposed from one side to other side by changing its sign.
- In cross multiplication, we multiply the numerator of LHS by the denominator of RHS
and the denominator of LHS by the numerator of RHS and the resultant expression are equal to each other. - Practical problems are based on the relations between some known and unknown quantities. We convert such problems into equations and then solve them.