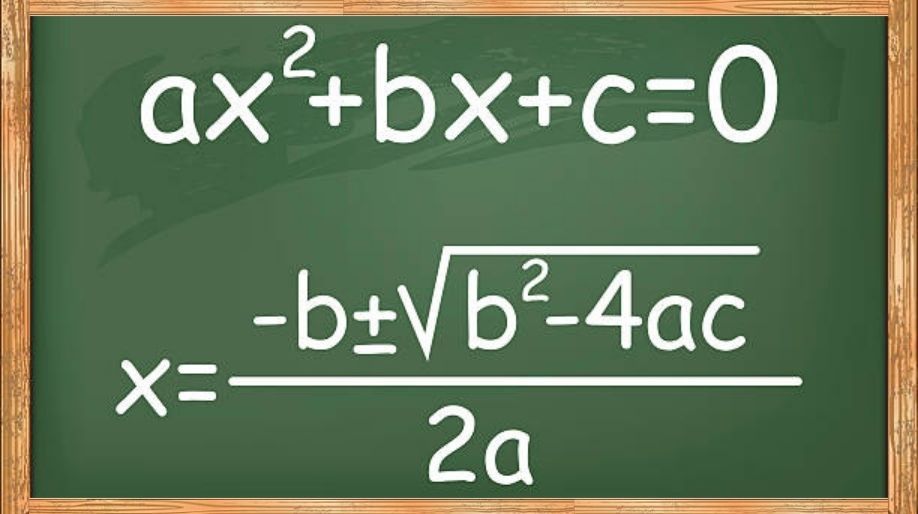The beauty of mathematics can be easily justified with the example of real life entities. Whatever we learn has some practical application or we can say that each and every practical situation has a mathematical solution. Interested to know how, lets discuss then how quadratic equations are used in our life.
An equation of second degree that is atleast on term will have a power of 2 is called as a quadratic equation.
The general or standard form of a quadratic equation in variable x is “ax2 + bx + c" where a, b and c are real numbers and a≠0.
Example 1: 2x2+3x+5=0, 3x2+7x+3=0 etc., are all quadratic equations.
- In general we say that any equation of the form p(x) = 0, where p(x) is polynomial of order 2 is called as a quadratic equation.
Example 2: The product of two consecutive integers is 72. Find the integers. For finding the integers derive a quadratic equation.
Solution: Let the first integer be = x.
Therefore the next consecutive integer = x +1.
Hence according the question
x(x+1) = 72
x2+ x-72=0 is the required quadratic equation.
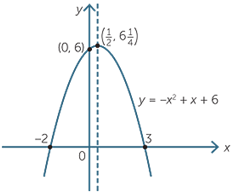
- The graphical representation of a quadratic equation solves a many real life problems like the movement of pendulum, the trajectory of a ball if we throw it vertically etc.
Solution of a Quadratic Equation
Let us assume a quadratic equation x 2-2x +1=0. On putting x=1 in the above equation we get 12-2+1 = 0 and hence the LHS also becomes 0 and equal to RHS and hence we say that 1 is a root or solution or zero of the above quadratic equation.
Generally we say that any real number α is said to be a root or solution of the quadratic equation ax2+bx+c=0 is α satisfies the quadratic equation that is aα2+bα+c=0. And hence α is also called as the zero of the above quadratic equation.
- Since the quadratic equation is of order two hence it will have maximum two roots or two solutions.
The roots of a quadratic equation can be obtained by two methods:
- Factorization method.
- Method of completing the square.
For ax2+bx+c in factorization method we try to resolve the middle term (b) into the factors of ac.
For ax2+bx+c in method of completing the square we try to make the quadratic equation a perfect square by certain manipulations.
Example 4: Find the roots of the quadratic equation x2-5x+6.
Solution: On splitting the middle term in -2x-3x
As [(-2x) x (-3x) = 6x2 = (x2) x(6)]
Therefore it can be written as x2 -2x-3x+6
= (x2 -2x)-(3x-6)
= x(x-2)-3(x-2)
=(x-2)(x-3)
Hence the roots or zeroes will be x=2 and x=3.
Quadratic Formula
Let us consider a quadratic equation ax2+bx+c=0 where a≠0.
Then the formula becomes
In the above equation entity is called as Discriminant of a quadratic equation.
The existence of roots of a quadratic equation totally depends on the discriminant of a quadratic equation.
So, a quadratic equation ax2+bx+c=0 has
- Two real and distinct roots if > 0.
- Two equal roots if = 0
- No real roots if < 0.
Here important points to be remembered are:
- For roots to real that is for real solutions b2-4ac ≥ 0.
- x sustains two values which are
- The two values of x thus obtained are known as the roots of the quadratic equation ax2+bx+c=0.
Solved Examples
Example 5: If a rectangular park has a perimeter of 40m and area of 200m2 then find the length and breadth of the park.
Solution: Let the length of the park be = x
Therefore Perimeter = 2(x+ breadth) = 40
Therefore breadth = 20 – x.
Therefore area = 200 = x(20 – x)
200 = -x2+20x
Therefore the equation becomes
x2-20x+200=0
Here a= 1, b=-20, c=200;
Now = 400 -800 = -400 < 0
Hence it proves that no such park can exist of such dimensions.
Example 6: A natural number, when increased by 12, equals 160 times its reciprocal. Find the number.
Solution: Let the natural number = x
Therefore according to the question
x+12 =
Hence the equation becomes x(x+12)=60
x 2+12x-160=0
Here a=1, b=12, c=160
Discriminant b2-4ac = 144 +640 =784 > 0
Hence the roots will be real and distinct:
And on putting the values in quadratic formula we get
x = 8 and x = -20.
As we know that a natural number cannot be negative and hence the answer is x = 8.
Practice Questions
Q1) Which of the following is a quadratic equation?
- x2+3x+4
- 3x+4
- 3-12x2=5x
- 4x2-3x3=45
Q2) Write the values of a, b and c for the following quadratic equations and hence find the value discriminant.
- 2x2-2x+9=0
- –x2+3x-8=0
- 5x2-24x+78=0
Q3) Check whether the quadratic equation 3x2+7x-10 has real roots or not. If yes find them.
Q4) A train travelling at a uniform speed for 360km, would have taken 48 minutes less to travel the same distance if its speed were 5km/h more. Find the original speed of the train.
Recap
- A quadratic equation in variable x is of the form ax2+bx+c=0 where a, b, c are all real numbers and a≠0.
- The graph of a quadratic equation is always a parabola.
- A real number α is said to be the root of the equation of the ax2+bx+c=0 if aα2+bα+c=0.
- The zeroes and roots of a quadratic equation are same.
- A quadratic equation can have a maximum of two roots.