What is Number System and Integers? In mathematics we always follow a systematic format whether it is for figures or for numerals also. It makes the things more generalize and hence more easy to understand. Here we are going to learn about the systematics of numbers and integers in the field of mathematics.
In the field of mathematics we follow two types of number systems which are:
1) Hindu Arabic Number System
2) Roman Number System
Hindu Arabic Number System
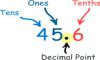
The most commonly and popular form of number system used in the field of mathematics is the Hindu Arabic number system because it is very easy to learn and also because of the simplicity of the number system.
It is a positional decimal numeral system that is the most common system for the symbolic representation of numbers in the world.
Numerals from 0 to 9 are used in the number system as base and the rest of the number are formed by combinations of these and by certain manipulations also.
- The numbers 0 – 9 are called as digit.
- The numbers created by their combination is numeral.
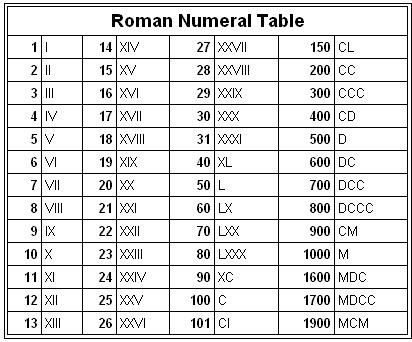
Roman Number System
The numbers from 0 – 9 and also their magical combinations can also represented using certain alphabets and this representation is called Roman Number System.
Classification of Numbers
Now we will learn more about how the numbers are classified and what are these classifications:
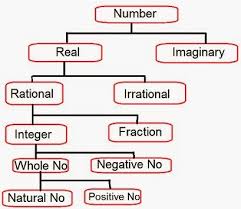
Real Numbers
All the numbers which can be represented on a number line are called as Real numbers. These are the set of the entire numbers positive, negative, integers, fractions or any number which has the existence and can be represented on a number line.
Example: 1, 45, 67/2, √5, etc.
Imaginary Numbers
Those numbers which cannot be represented on the number line are called as imaginary numbers. You all will learn about this in higher classes.
Example: 3+2i, 5-i, 8i, etc.
Rational Numbers
Numbers which can be written in the form of p/q where p and q both are integers and q ≠ 0 is called as a rational number.
Example: 1, 3/2, 4/5, 12, etc.
Irrational Number
Numbers which cannot be written in the form of p/q are known as irrational number. In simple words all those real numbers which are not rational are irrational numbers.
Example: √5, 1+√2, 5+√3, √3, etc.
Fractions
The part of a whole is known as Fraction where the whole can be a single object or can be group of objects.
All those numbers which are written in the form of p/q where p and q must be integers and q are called as fractions.
Example: ½, 3/2, 4/5, 7/8, 8/4,etc.
Integers
The rational numbers which don’t have their fraction parts are called as integers. In simple words, all those rational numbers in which the denominator is 1 or q=1 are called as rational numbers.
Example: 1, 2, 3, 5, -9, 45, 564, -7,-3, etc.
Integers are classified in two categories:
- a) Positive Integers: All those numbers which are greater than 0 are called as positive integers. They are represented on the right side of the number line that is after 0.
Example: 1, 2, 3, 59, 256, 7845, 52148, etc.
- b) Negative Integers: All those numbers which are less than 0 are called as negative integers. They are represented on the left side of the number that is line before 0.
Example: -1, -2, -5, -78, -456, -9841, etc.
All the positive integers can be classified as:
- a) Whole numbers: All those numbers starting from 0 are called as whole numbers.
- b) Natural numbers: All those numbers starting from 1 are called as natural numbers.
- All the natural numbers are whole numbers.
- All the whole numbers are natural numbers except 0.
Recap
- All the numbers in mathematics are arranged in a set of real numbers and hence are called as number systems.
- All those numbers which can be represented on the number line are known as real numbers.
- Numbers which can be written in the form of p/q where p and q are both integers and q≠0 are called as rational numbers.
- Rational numbers in which q=1 are called as integers and if q≠1 then they are called as fractions.
- All natural numbers are whole numbers but vice versa is not true.