What is coordinate geometry? In mathematics each and every point or any figure plane or anything has a specific position in space. To locate a point we require proper coordinates of the point. And these coordinate represent the position of the point. Here we will learn about the geometries through the coordinates.
The determination of the coordinates of any figure, plane or any point in space and application of the various geometries on these figures is called as Coordinate Geometry.
Below are some basics related to Coordinate Geometry:
Distance Formula x-coordinate, or abscissa. y-coordinate, or ordinate. (x, 0), and of a point on the y-axis are of the form (0, y). Let us consider two points in the Cartesian plane P and Q. The coordinates of P(x1,y1) and Q(x2,y2). Then the distance between the two points P and Q will be given by the Distance Formula PQ =√ [(x2-x1 )2 + (y2-y1)2] OR (PQ)2 = (x2-x1 )2 + (y2-y1)2 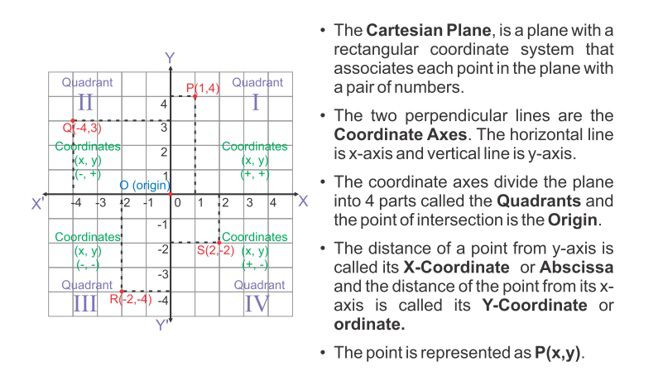

Solution: Since the point is on X axis let us assume it’s coordinates is (x,0).
Therefore, on using the distance formula we get,
(2-x)2 + (-5-0)2 = (-2-x)2+ (9-0)2 (On squaring both the sides)
4+x2-4x + 25 = 4+x2+4 x + 81
8x = 56 and hence, x = 7.
Therefore, the point (7,0) is the point on X axis equidistant from the above two points.
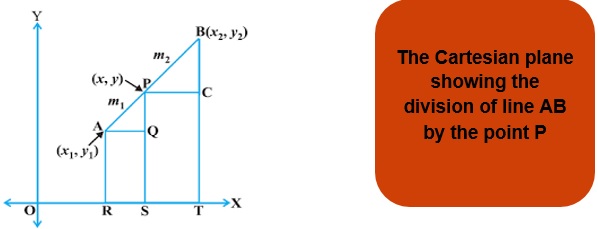
Section Formula
Let us suppose two points A(x1,y1 ) and B(x2,y2) on the Cartesian plane. If any point P(x,y) divides the line segment AB in the ratio m:n then the coordinates of P(x,y) cab be find using the section formula:
When division is internal:
x = (mx2+ nx1 ) / (m+n) and y = (my2+ ny1 ) / (m+n)
When division is external:
x = (mx2- nx1 ) / (m-n) and y = (my2-ny1 ) / (m-n)
Here an important point is to be remembered that if P is the mid-point of the line segment AB, then the value of both m and n will be that is the ratio will be 1:1
Example 2: Find the coordinates of the point which divides the line segment AB in half where A(-2,2) and B(2,8).
Solution: Let us assume the coordinates of the point to be (x,y) and here m:n = 1:1.
So by using the Section Formula we get:
x = [(1 x 2) + (1 x -2)] / (1+1) and y = [ (1 x 8) +(1 x2)] / (1+1)
x = 0 and y = 5
Hence the point (0,5) divides the line AB into half.
Area of Triangle
We all know the very basic formula to calculate the area of a triangle whose bas e and height is given by:
Area = x Base x Height
We also know the other method to calculate the area of the triangle by using the Heron’s Formula. But here in coordinate geometry we are going to learn another formula or way to calculate the area of a triangle:
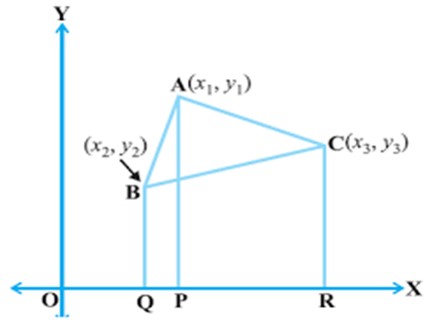
Let us suppose three points in the Cartesian plane A(x1,y1 ) B(x2,y2) and C(x3,y3) . Hence the area of the triangle ABC formed by joining these three points will be given by:
Area = ½ [ x1(y2 -y3) + x2(y3 -y1) + x3(y1 –y2)]
Example 3: Find the area of the triangle with vertices (1,1) (2,2) and (3,3).
Solution: By using the formula we get
Area = ½[1(2 – 3) + 2(3-1) + 3(1-2)] = 0.
Here the area of triangle is 0, which means these three do not form a triangle which means they are collinear.
Hence we can check whether three points are collinear or not bye finding the area of the triangle and if it comes to be 0 then they are collinear otherwise not.
Practice Questions
Q1) Find the distance between two points A(4,5) and B(5,-8).
Q2) Show that the points A(0,-1), B(-2,3), C(6,7), D(8,3) are the vertices of a square.
Q3) Find the point on y axis which is equidistant from the point (5,5) and (3,-2).
Q4) Find the coordinates of the point P which divides the line segment A(3,4) and B(8,2) in the ratio 2:3.
Q5) Find the area of the triangle with vertices (5,4) , (7,1) and (4,2).
Recap
- Distance formula can be used to calculate the distance between two points on a Cartesian plane.
- Section Formula is used to find the division ratio which a point makes on any line segment.
- If we have given three points then we can also calculate the area of the triangle formed.
- If the area comes out to be 0 we can predict that these three points are collinear. This helps us a lot in further investigations of the figures which you will learn in higher classes.