Trigonometry

According to J.F. Herbart “There is perhaps nothing which occupies the middle position of mathematics as trigonometry". From the statement itself we can guess that what a great or important role trigonometry plays in Mathematics. Let’s start from the beginning and learn how interesting it is.

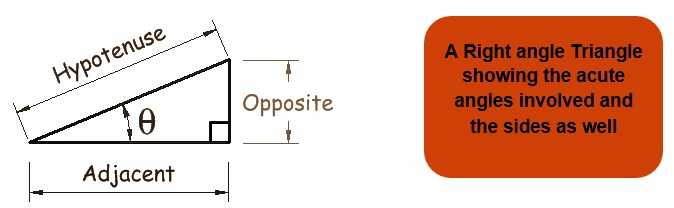
Trigonometry is basically the measuring of sides, angles and other things involved in a triangle and here we will deal with right angle triangle, the angles involved and many other things.

Trigonometry is derived from Greek words “tri" means three “gon" means sides and “metron" means measurements.

Here we will study the different Trigonometric Ratios different terms identities related to Trigonometry.

Trigonometric Ratios

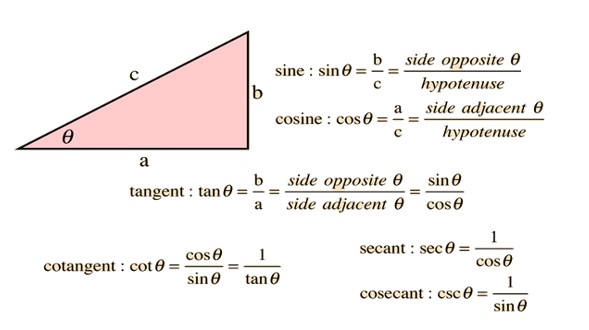
Here in any right angle triangle we define 6 trigonometric ratios which are Sine, Cosine, Tangent, Secant, Cosecant, and Cotangent.

So, the trigonometric ratios of an acute angle in a right triangle express the relationship between the angle and the length of its sides.

For any Triangle ABC we define the trignometric ratios as:

Example 1: Find the value of all trigonometric ratios at angle A, if in any triangle ABC right angled at B AB=24, BC=7.

Solution: For any right angled triangle
using Pythagoras theorem we get

AB²+BC²=AC²

24²+7²= AC² and hence AC =25.

Therefore from the figure

Sin A = 7/25 Cosec A = 25/7

Cos A = 24/25 Sec A = 25/24

Tan A = 7/24 Cot A = 24/7

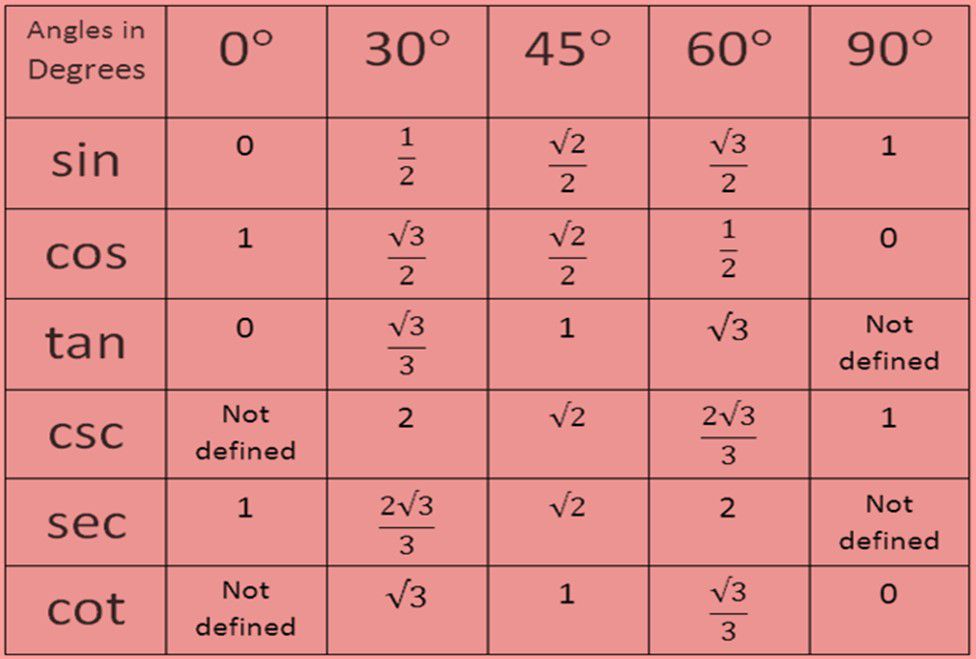
Trigonometric Ratios for some specific Angles

If we take a triangle ABC and then if we assign the values of

When we standardize the value of θ with some of the values then we get some results which are very helpful for us and are shown in the following table:

Example 2: If the value of Tan (A+B) = √3 and the value of Tan(A-B) = 1/√3. And 0°

Solution: As we know that Tan 60° = √3 and Tan 30°= 1/√3.

Hence we can conclude then that:

A+B = 60° and A-B = 30° and on solving we get

A = 45° and B =15°.

Complementary Angles

Two angles are said to be complementary when their sum is 90°. Here we will discuss the complementary angles of some trigonometric formulae’s:

1. i) Cos(90°-A) = Sin A ii) Sin(90°-A) = Cos A

iii) Tan(90° -A) = Cot A iv) Cot(90°-A) = Tan A

1. v) Sec(90°-A) = Cosec A vi) Cosec(90°-A) = Sec A

Example 3: If Tan A = Cot B then prove that A+B = 90°.

Solution: As we know that Cot B = Tan (90°-B)

Tan A = Tan (90°-B) and hence we get that

A = 90° - B

Therefore, A+B = 90°. (Hence Proved)

Trigonometric Identities

1) Cos² A + sin² A = 1

2) 1 + tan² A = sec²A for 0°≤A≤90°

3) Cot² A +1 = cosec² A for 0°≤A≤90°

Applications

If we study more about the history of the evolution and birth of trigonometry we get so many proofs of the existence of the uses of angles and thus the trigonometry involved. The basic and the most historic example is the Pyramids in Egypt.

Another big and bold example is of Theodolites which is based on the principle of trigonometry itself. Theodolite is an instruments used by civil engineers for the purpose of surveying.

The major use of trigonometry which we will study is to find the height and distance between two distant objects and we will study some basic points of how we locate ships from Light houses and a lot more.

Let’s learn some basic terminologies which we are going to discuss:

Line of Sight: The line of sight is drawn from the eye of an observer to the point in the object viewed by the observer.

Angle of Elevation: The angle of elevation of an object viewed, is the angle formed by the line of sight with the horizontal when it is above the horizontal level, i.e., the case when we raise our head to look at the object.

Angle of Depression: The angle of depression of an object viewed, is the angle formed by the line of sight with the horizontal when it is below the horizontal level, i.e., the case when we lower

our head to look at the object.

Practice Questions

Q1) Prove that (1-cos²A) cosec²A = 1.

Q2) Prove that (1+cosA)(1-cosA)(1+cos²A) = 1.

Q3) Prove that (1+tan²A)(1+cot²A) (sin²A-sin⁴A) = 1.

Q4) State True or False:

1. a) sin A = cos(90°-A)
2. b) sin²A + 1 = cos²
3. c) tan²A + 1= sec²

Recap

• In trigonometry we deal with all the angles, lengths and various measurements using some ratios called as trigonometric ratios.
• The important identities are

1) Cos² A + sin² A = 1

2) 1 + tan² A = sec²A for 0°≤A≤90°

3) Cot² A +1 = cosec² A for 0°≤A≤90°

• The major application part of trigonometry can be used for heights and distance for distant objects using the concept of the angle of depression and angle of elevation.