In our day to day life, we all come across so many objects which are the exact replica of each other.

  • Like when we see certain figures with evenly balanced proportions, we say, “They are symmetrical".
  • Here we are going to see and learn the about the concepts of symmetry and its practical applications.
  • In mathematics symmetry means that one shape becomes exactly like another when you move it in some way: turn, flip or slide or you see it any manner at any angle they will be the exact replica of each other. 

Line of Symmetry 

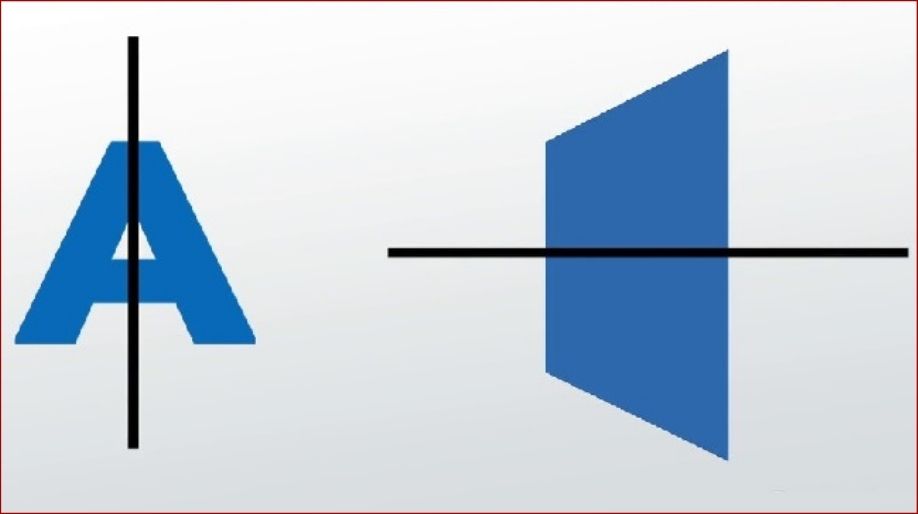
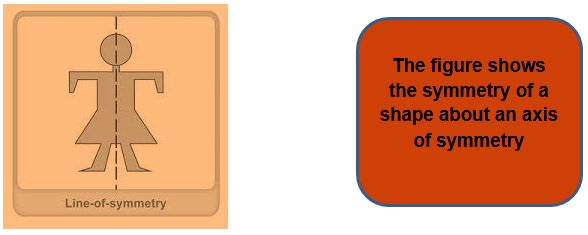
  • A line of symmetry is also called an axis of symmetry.
  • We always talk about symmetry about any line or axis as there always have to be a base about which we are going to define the symmetry.
  • Thus the imaginary line about which we discuss the effect of symmetry is called as the line or axis of symmetry.
  • The axis of symmetry can be found in any direction any angle any position of the body but we just have to make sure that about the axis of symmetry the body has to be symmetric come what may.

Maths class 6 Symmetry and Practical Geometry  

  • A line of symmetry can be either horizontal, vertical, inclined at any angle.
  • A body can have multiple numbers of lines of symmetries.
  • Folding Test. You can find if a shape has a Line of symmetry by folding it. When the folded part sits perfectly on top (all edges matching), then the fold line is a Line of Symmetry.
  • So the square has four lines of symmetry. The rectangle has only two, as it can be folded in half horizontally or vertically.

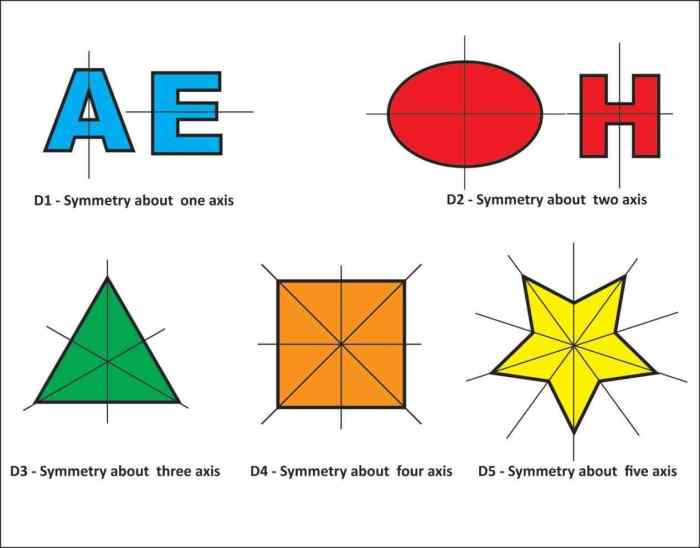
The following figure shows the different lines of symmetry in different figures and how we can obtain lines or axis of symmetry in different figures.

Maths class 6 Symmetry and Practical Geometry

Reflection and Symmetry

  • Reflection and symmetry have a very close relationship as they are totally related to each other in terms of their properties and their appearance.
  • Reflection is a type of symmetry where one half is the reflection of the other half.
  • A figure which does not change upon undergoing a reflection has reflection symmetry.

Mathematical Instruments

Here we are going to learn more about the instruments which we use in the field of mathematics to draw various shapes.

1) Scale: It is a basic instrument which can measure in mm, cm, m according to the markings on it.It is mainly used to draw a straight line and also to measure the length of it.

2) Compasses: It is a basic instrument consists of a pencil and a pointer and is used to mark off equal lengths and also sometimes to cut off arcs.

3) Divider: It is a basic instrument and consists of two pointers and is used to compare lengths.

4) Set Square: It is a basic instrument which consists of a triangle of 45°, 45° and 90° angle and another triangle of 30°, 60° and 90° angles and is used to draw perpendicular and parallel lines.

5) Protractor: It is a basic instrument of semicircular shape and can measure angles in degrees from 0° to 180°.

  • Using the ruler and compasses we can make the following constructions:

1) A circle, when the length of its radius is known.

2) A line segment, if its length is given.

3) A copy of a line segment.

4) A perpendicular to a line through a point

  1. a) On line (b) not on the line.

5) The perpendicular bisector of a line segment of given length.

6) An angle of a given measure.

7) A copy of an angle.

8) The bisector of a given angle.

9) Some angles of special measures such as

             (a) 90° (b) 45° (c) 60° (d) 30° (e) 120° (f ) 135°

Practice Questions

Q1) Find all the lines of symmetries of all the 26 alphabets

Q2) Find the reflection symmetry of all the basic elementary shapes like square, rectangle etc.

Q3) How will you draw a circle with the help of a compass?

Q4) Can we measure the length of a line segment with the help of a compass?

Recap

  • A figure has line symmetry if a line can be drawn dividing the figure into two identical parts. The line is called a line of symmetry.
  • The line symmetry is closely related to mirror reflection. When dealing with the mirror reflection, we have to take into account the left-right changes in orientation.
  • Symmetry has plenty of applications in everyday life as in art, architecture, design creations, geometrical reasoning, Rangoli, textile technology etc.