Math Magic Tricks
There are many maths tricks that you can use to play math magic tricks. Learn the magic trick of digital roots.
The Magic:
One time, lightning struck your computer, and your brain temporarily fused with the Internet. Your mind gained supercharged computation powers, but because it's the Internet, you only use them to tell other people they're wrong.
To demonstrate this, you tell them to grab a calculator, multiply random four-digit numbers, and write down the results, but intentionally write some of them wrong. Common mortals wouldn't be able to tell the difference, but you're not a common mortal, so you briefly glance at each problem and tell them which ones were changed. They never doubt your powers again and become your butlers.
The Math:
The secret is so ancient that it was already old by the 10th century, and so useful for double-checking your homework that you might have learned it in school and just forgot. Let's take the following problem:
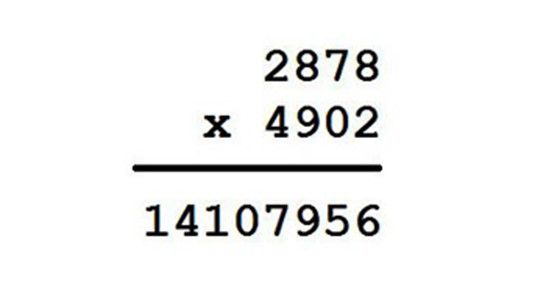
The Magic:
At your local bookstore, you spot an attractive somebody carrying the exact same book as you; because it's the only book they sell (it's a bad bookstore). He or she seems a little skeptical when you say this means you must be soul mates, so you offer to prove it with a magical gesture worthy of a John Cusack rom-com.
- Pick a starting page, and each of you secretly chooses any word from the first line.
- Silently spell it out and move one word forward for each letter.
- So if you start with the word "throbbing," move nine words forward; if you land on "moaned," move six words.
- Do that until you reach the end of the page.
At the end, announce the word you landed on: "explodegasm." Amazingly, even though you didn't know which word the other person started from, your journeys ended on a mutual explodegasm. It must be destiny!
The Math:
Or, you know, just simple arithmetic. The secret is based on the Kruskal count, which isn't the name of a magic-wielding vampire, but of a mathematical parlor trick discovered by physicist Martin Kruskal. Essentially, no matter which word you started from, if the text on the page is long enough (don't do this with a Dr. Seuss book), you'll both hit the same word at some point, and from then on the paths will be the same.
Magicians use this all the time. Here's the Kruskal method illustrated with cards –
 >
>
Yellow and blue start separately but inevitably meet up on the four of clubs:
So really, your amazing connection was based less on some mystical love voodoo and more on cold, mathematical certainty.
Is that result right or wrong? No clue. Unless that is, we were to make all those scary numbers more manageable by simply adding up their digits:
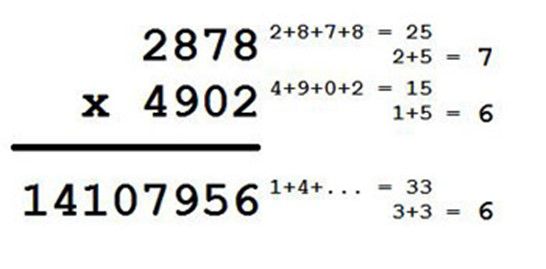
Those are the numbers' digital roots -- sort of like the spokesperson of each number that can represent it when it can't be bothered to leave the house. So, instead of multiplying the big four-digit figures, we can multiply the roots instead. If the roots of the question and the answer match, congratulations, the answer is right! If not, then someone's lying or wrong.
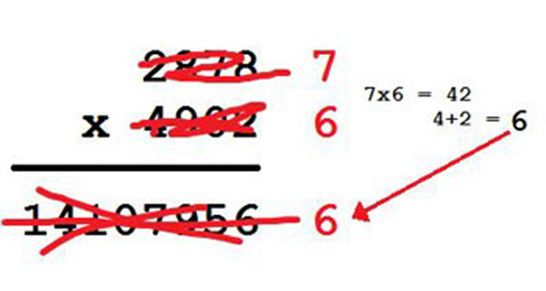
This method is called casting out nines, and there's an even bigger mind game you can pull off with it:
- Tell your spectators to take any long number (let's go with 6,969).
- Rearrange it to make another number, and then subtract the smaller number from the larger one (9,966 - 6,969 = 2,997).
- The digital root will always be 9, for some reason.
- Now instruct them to multiply the result by another figure, as big as they want (say, 8,008,135).
- Finally, have them choose one digit as their secret number, and give you the others.
They'll be like "I just spent half an hour mixing, subtracting, and multiplying random numbers. No way you can guess that number." Unless you add up all the digits and subtract the result from 9 (because that's still the root), like this:

Boom, secret number. You can draw some alchemical symbols or something to spruce up the presentation, but we're guessing it won't be necessary. They'll be scared enough of you as it is.
Trending:
| Free preparation material for Maths Olympiad |
| Quick Maths definitions that everyone should know |
| All the Maths tricks that you can not miss |
| NCERT Solutions for all the subjects |

 Digital Roots: The U..
Digital Roots: The U..
 Faster Percentage Ca..
Faster Percentage Ca..
 Quickly Calculate Th..
Quickly Calculate Th..
 5 Maths Tricks..
5 Maths Tricks..
 5 Time Saving Maths ..
5 Time Saving Maths ..
 Perfectly Sort Coins..
Perfectly Sort Coins..
 Fake A Mystical Lite..
Fake A Mystical Lite..
 Quick Mathematics Tr..
Quick Mathematics Tr..