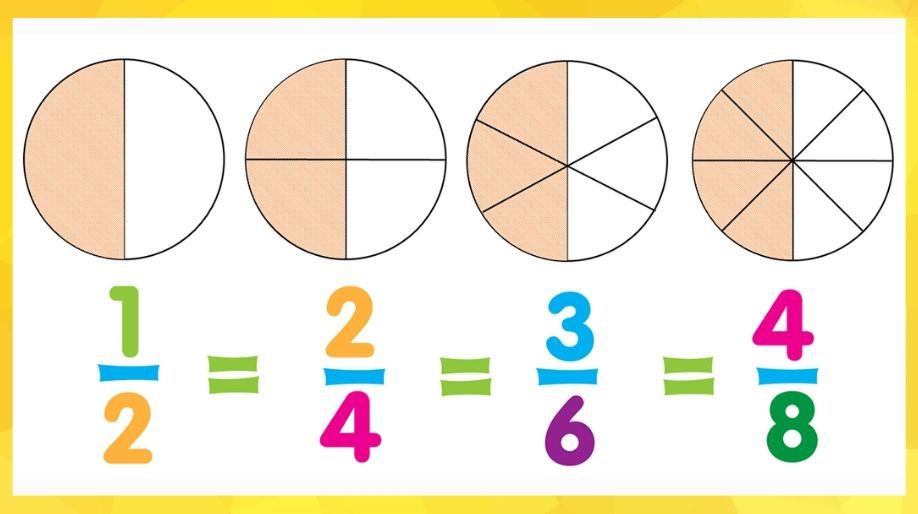We all have heard of this word in the field of mathematics as well as in our everyday lives. For example when we eat half apple, it’s a fraction, if we eat ¼ of apple it’s also fraction. Let us just find what actually it is.

Maths class 3 Fractions

The part of a whole is known as Fraction. For example if a watermelon is cut into 4 parts then each part will be a fraction of the whole watermelon.

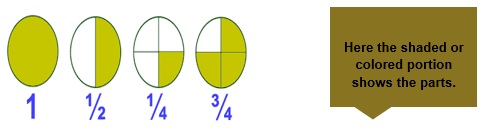
Maths class 3 Fractions

Understanding Fractions

A fraction consists of two parts:-

  1. Numerator: The part which is written above the horizontal line is called as numerator.
  2. Denominator: The part which is written below the sleeping line horizontal line is called as denominator.

Thus, a number is written above and a below the horizontal line and then the arrangement is called as fraction.

Example 1: As we know that 1 /2 is a fraction where 1 is the numerator and 2 is the denominator and the whole ½ is called a fraction.

Types of Fractions

There are three types of fractions:

  1. Proper Fraction: Fraction whose numerator is less than the denominator is called a proper fraction.

Example 2: 3/4, 7/8, 2/5, 5/7, etc.

  1. Improper Fraction: Fraction whose numerator is either equal or greater than the denominator.

Example 3: 3/2, 5/4, 8/7, 11/11, 2/2, etc.

  1. Mixed Fraction: A combination of a whole number and fraction together is called mixed fraction.

Maths class 3 Fractions

Example 4: There is method of solving mixed fractions and by this we convert the mixed fraction into improper fraction.

Example 5: Solve the above example.

Solution: To solve this we will follow 3 steps

  • Multiply the whole no. with denominator. (2 x 3 = 6).

  • Add the answer obtained in step 1 to the numerator

(6 +1 = 7).

  • Place the result obtained in step 2 in the place of numerator and the denominator remains the same.

Hence the fraction becomes 7/3 which is an improper fraction.

There is another category of fractions called as

Equivalent Fractions: Those fractions which look different but on solving becomes same.

Example 6:- 1/3 and 2/6. Here 2/6 can be written as 2/2 x 1/3.

And 2/2 =1 therefore 2/6 comes up to be 1/3.

Another example is 1/2 and 2/4.

Comparing Fractions

Comparing means to find out some characteristics like which one is greater and which is small when two or more numbers are observed together.

Here we are going to compare two fractions whose denominators are same and it can be done in the following steps:-

  • Observe that the denominator of both the fractions is same.

  • Now observe the numerator, the fraction whose numerator is greater will be the greater fraction.

Example 7: Compare who is greater 3/7 or 5/7?

Solution: Here both the fractions have the same denominator and hence on observing the numerators we get that 5 is greater than 3 there 5/7 is greater than 3/7.

5/7 > 3/7.

Computing operations on fractions

As we all know that addition, subtraction, multiplication and division are the computing operations.


Here we are going to study only the first two computation operations on fractions.

Addition and Subtraction of Fractions

Two fractions with the same denominator can be added or subtracted by using the two steps:

  • Observe that the denominators of both the fractions are same.

  • Add or subtract the numerators as asked in the questions.

Example 8: Add and subtract 4/5 and 3/5.

Solution: As we can see the denominators of both the fractions is same and hence we can add and subtract them by using the numerators.

Therefore, 4/5 + 3/5 = 7/5 and 4/5 – 3/5 = 1/5.

Practice Questions

Question 1:- What is 3 parts of 4 and how will you write it?

Question 2:- Which one is smaller 11/13 or 15/13?

Question 3:- Solve the mixed fraction 5 ½.

Question 4:- State True or False:

  1. 3/4 > 1/4.
  2. 5/9 = 10/18.
  3. 12/13 < 9/13.
  4. 13 /15 is an improper fraction.
  5. 15/15 is a proper fraction.
  6. 15/17 is a proper fraction.

Question 6:- Compute the answers of the following:

  1. 4/3 + 5/3 = ?
  2. 17/12 – 5/12 = ?
  3. 5/2 + 1/2 = ?

Recap

  • The part of a whole is fraction.
  • Numerator and denominator are the parts of a fraction.
  • Fractions can only contain integers
  • If denominators are same then we can compare the fractions by comparing the numerators.
  • If Numerator > or = Denominator then improper fraction.
  • If Numerator < Denominator then proper fraction.