• Any number that can be expressed in the form a/b, where a and b are integers and b≠0 is called a rational number.

For example:4/7,2/3,-6
are all rational numbers.

Addition of rational numbers

To add two rational numbers, first express each rational number with a positive denominator.

• Associative Property: If a/b, c/d, and e/f are three rational numbers, then [(a/b + c/d) + e/f] = [a/b + (c/d + e/f)]

Subtraction of rational numbers

Subtracting one rational number from another rational number is same as adding the additive inverse(negative) of the rational number that is being subtracted to the other rational number

EXAMPLE 1: Sum of two rational number is 1/6. If one of them is -1/2, then find the other rational number.

SOLUTION: The other rational number is = 1/6 – (-1/2) =1/6 + ½ = 2/3 [ANS]

EXAMPLE 2: What number should be added to -1/4 to get -4/5?

SOLUTION: The number is = -4/5 – (-1/4) = -4/5 + ¼ = -11/20 [ANS]

Multiplication of rational number

• To multiply two rational numbers proceed as under:
  Multiply the numerators together and the denominators together, place the products of numerators above the products of the denominator.
  

• The number 1 is called the multiplicative identity of rational numbers.
  
  

• Multiplication is distributive over addition and subtraction.

• To divide one rational number by another(non-zero) rational number proceed as under:
  Multiply the dividend by the reciprocal of the another

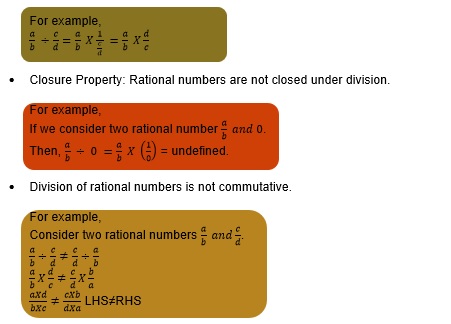
• Division of rational numbers is not associative.

Representation of a rational number on a number line

To represent rational number on a number line proceed as under:

Rational numbers between two rational numbers

To insert n rational numbers between two rational numbers, do the following:

• When given rational numbers have the same denominator multiply the denominator and numerator by (n+1).
• When given rational numbers have different denominators: find the LCM of the denominators; change the given rational number into equivalent rational numbers with LCM as their denominator; If necessary multiply the denominator and numerator of each by (n+1).

Practice these questions

Q4) Vivan donated of his salary to the orphanage, 1/4^th of his salary on food, 1/3 of his salary on rent and electricity, and 1/15^th of his salary on telephone bills. This month he donated Rs. 6000 in a charity. He is left with Rs. 4000. Find his monthly salary.

Q5) Area of a square is 1 sq. metre more than ½ of the area of a rectangle. If the area of the square is 91 sq. metre. Then find the dimensions of the rectangle. Given breadth is ¾ times of length.

Recap

• A number that can be addressed in the form a/b where a and b are integers and b≠0, then the number is a rational
• All integers and fractions are real numbers
• All decimals except non-terminal and non-recurring are rational numbers
• Addition is closed, commutative, associative.
• Subtraction is closed. But neither commutative nor associative.
• Multiplication is closed, commutative, associative and distributive

Division is not closed, not commutative, not associative.