We all observe different shapes of triangles in our day to day life. Like for example, the two set squares of our geometry box are both triangles.

  • But here on comparing these two triangles, we observe certain properties and here we are going to discuss the same about the triangles and circles.
  • In triangles, we have observed that there are a lot of similarities between triangles like condition for triangles to be congruent which means they have same shape and size.
  • But what about those triangles who don’t have same shape size? Do they also have any relation between them? Let’s find out.

Similarity of Triangles

  • Two triangles having the same shape but not necessarily the same size are called as similar triangles.

Two triangles are similar, if:

 

  • Their corresponding angles are equal and
  • Their corresponding sides are in the same ratio (or proportion).
  • If the corresponding angles of a triangle are equal then it is said to be an equiangular triangle.
  • It is very important to note that every congruent triangle is similar but vice versa is never true.

Criteria for Similarity of Triangles

There are certain criteria on whose behalf we decide whether triangles are similar and these are:

  1. a) AAA Criterion: If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio and hence the two triangles are similar (AAA similarity criterion).

 

  1. b) AA Criterion: If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.

 

  1. c) SSS Criterion: If in any two triangles the side of one triangle is proportional to the side of other triangles, then their corresponding angles will be same and hence the triangles will be similar.

 

  1. d) SAS Criterion: If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.

Here an important point has to be discussed about the area of the similar triangles which is mentioned below:

 

  • The ratio of the areas of the two similar triangles is equal to the square of the ratio of their corresponding sides.

The following figure shows the similarity of two triangles ABC and DEF under the AAA criterion of similarity of triangles.

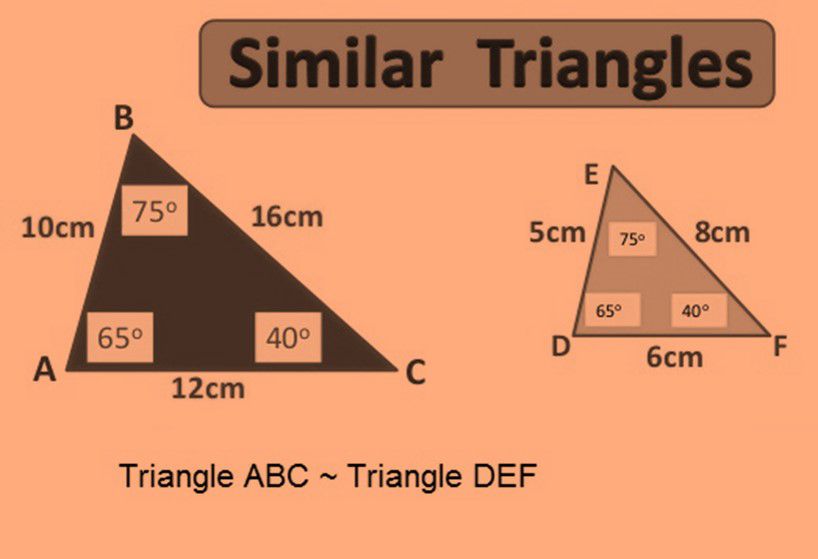
Maths class 10 Triangles Circles and Construction

Example 1: Two triangles ABC and DEF are as shown in the figure. Predict whether they are similar or not.

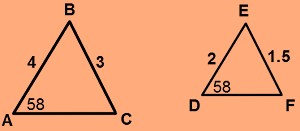
Maths class 10 Triangles Circles and Construction

 

Solution: Here the sides AB and DE and the sides BC and EF are proportional to each other and angle A is equal to the angle D.

Hence with SAS criterion both the triangles, ABC and DEF are similar to each other.

Triangle ABC ~ Triangle DEF

Pythagoras Theorem

 

  • This theorem was given by Pythagoras which states that if a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.

 

  • Its application is that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

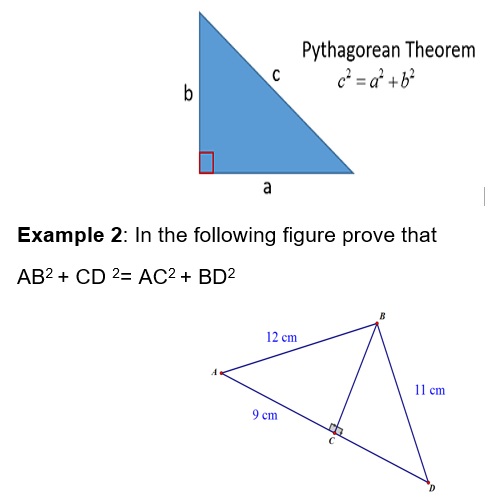
Maths class 10 Triangles Circles and Construction

Solution: In the figure on using Pythagoras theorem in triangle ABC and BCD we get

AB2 = AC2 + BC2   and

BD2 = BC2 + CD2

On subtracting both the equations we get

AB2 – BD2 = AC2 – CD2

Therefore,

AB2 + CD2 = AC2 + BD2 (Hence Proved)  

Circles

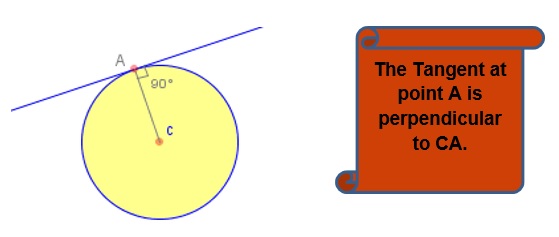
Tangent: When any line just touches a circle or intersects the circle at one point only then the line is said to be tangent to the circle.

Secant: When any line segment intersects the circle at two distinct points, the line is said to be secant to the circle.

  • Tangent to a circle is a special case of secant where the two intersecting points coincide.
  • The Tangent at any point to the circle is always perpendicular to the radius vector at that point. 

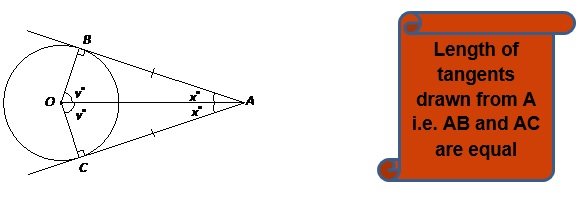
Maths class 10 Triangles Circles and Construction

 

  • A circle can have any number of tangents but if we talk tangent at a point, then it can have only one.
  • The lengths of tangents drawn from an external point to the circle are equal.

Maths class 10 Triangles Circles and Construction

        

Construction

  • In mathematics, we all frequently require to create certain figures or we have to represent some figures geometrically, but it is not very easy to create the accurate figure.
  • Hence we will use some basic steps of construction to obtain a correct geometrical figure.

Here we will learn the steps to make a tangent to a circle from an external point.

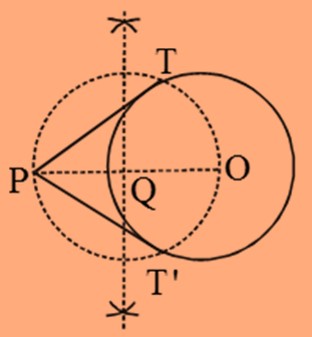
Example 3: Draw tangents to a circle of radius 4cm from a point outside it at a distance of 8cm.

Solution: We will follow the following steps of construction:

  1. a) Draw a circle of radius 4 cm with centre O.
  2. b) Mark a point P at 16 cm from O.
  3. c) Taking OP as diameter draw another circle such that it intersects the previous circle at T and T’.
  4. d) Join P to T and T’. The line segments PT and PT’ will be the tangents from P to the circle.

Maths class 10 Triangles Circles and Construction

Practice Questions

Q1) Draw a pair of tangents to a circle of radius 10 cm which is inclined to each other at an angle of 45°.

Q2) The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.

Q3) How many tangents can a circle have?

Q4) Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.

Q5) Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.

 

Recap

  • Two figures having the same shape but not necessarily the same size are called similar figures.

 

  • All the congruent figures are similar but the converse is not true.

 

  • If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

 

  • If in a triangle, square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
  • When any line just touches a circle or intersects the circle at one point only then the line is said to be tangent to the circle.
  • A circle can have any number of tangents but if we talk tangent at a point, then it can have only one.
  • The tangent to a circle is perpendicular to the radius through the point of contact.