Rational Numbers
- A number that can be addressed in the form a/b where a and b are integers and b≠0, then the number is a rational
- All integers and fractions are real numbers
- All decimals except non-terminal and non-recurring are rational numbers
- Addition is closed, commutative, associative.
- Subtraction is closed. But neither commutative nor associative.
- Multiplication is closed, commutative, associative and distributive
- Division is not closed, not commutative, not associative.
Linear equation in one variable
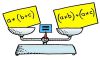
- The basic principle used in solving any linear equation is that any operation performed on one side of the equation must also be performed on the other side of the equation.
- Any term in an equation can be transposed from one side to other side by changing its sign.
- In cross multiplication, we multiply the numerator of LHS by the denominator of RHS
and the denominator of LHS by the numerator of RHS and the resultant expression are equal to each other. - Practical problems are based on the relations between some known and unknown quantities. We convert such problems into equations and then solve them.
Understanding Quadrilaterals and Practical Geometry
- The sum of all angles of a quadrilateral is 360°.
- When a parallelogram is divided by its diagonal we get two congruent triangles.
- Diagonals of a rectangle bisect each other and are equal and vice-versa.
- Diagonals of a rhombus bisect each other at right angles and vice-versa.
- Diagonals of a square bisect each other at right angles and are equal, and vice-versa.
- We can construct a quadrilateral if we know: four sides and a diagonal, two adjacent sides and three angles, three sides and two diagonals, three sides and two included angles.
Squares and square roots, Cube and cube roots
- If a number is multiplied by itself, then the product is said to be the square of the number
- No perfect square number can end with 2, 3, 7, or 8
- Perfect square numbers end with either 0 or 1 or 4 or 5 or 6 or 9.
- If a is a non-zero number then aXaXa written as a^3 is called the cube of a.
- If a number is negative then its cube is also negative i.e.,
- If n is even, then is also even.
Comparing Quantities
- Ratio tells us how much of one thing there is compared to another.
- Percentage is not cumulative in nature.
- Profit% and Loss% are always calculated with respect to Cost Price.
- Sales tax is collected by the retailer when the final sale in the supply chain is reached via a sale to the end consumer.
- VAT (Value-Added Tax) is collected by the seller at each stage of the supply chain.
- Compound Interest is the interest calculated on the initial principle and also on the accumulated interest of previous periods of a deposit or loan.
Algebraic Expression & Identities
- Algebraic expressions consist of numbers, variables and mathematical operators.
- A term can be a number, a variable, or a constant multiplied by a variable or variables. Each term in an algebraic expression is separated by a positive sign or negative sign.
- If algebraic expressions are expressed as the product of numbers, variables or expressions, then each of these numbers and expressions is called the factor of algebraic expressions.
- When a term of an algebraic expression is made up of a constant multiplied by a variable or variables, then that constant is called a coefficient of the algebraic expression.
- Algebraic expressions which contain one non-zero term only are called monomials.
- Algebraic expressions which contain two non-zero terms are called binomials.
Mensuration
- Curved Surface Area of cylinder =2 x pi x r x h
- Volume of the cuboid is given by, V=l×b×h
- Volume of a cylinder of base radius ‘r’, and height ‘h’ = (area of base) × h=